时间:2017-07-31 08:20:25
1、简答题 如图长L=0.5m质量不计的杆下端固定在O点,上端连着球A,球A质量为m=2kg,A绕O在竖直面做圆周运动.
(1)若小球A过最高点时速率若为1m/s,求此时球对杆的作用力大小和方向;
(2)若小球A过最高点速度为4m/s时,求此时球对杆的作用力大小和方向.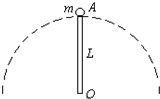
参考答案:(1)对小球受力分析,受重力、杆的弹力(假设向下),合力提供向心力,根据牛顿第二定律和向心力公式,有
mg+F=mv2L
代入数据,解得
F=mv2L-mg=-16N
负号表示此时球对杆的作用力方向与假设的方向相反,即向上,大小为16N;
根据牛顿第三定律,杆对球的弹力和球对杆的弹力方向相反、大小相等;
故此时球对杆有16N的向下的弹力.
(2)再次对小球受力分析,受重力、杆的弹力(假设向下),合力提供向心力,根据牛顿第二定律和向心力公式,有
mg+F=mv2L
代入数据,解得
F=mv2L-mg=44N>0,即假设成立,杆对球的弹力向下;
根据牛顿第三定律,杆对球的弹力和球对杆的弹力方向相反、大小相等;
故此时球对杆的作用力向上,大小为44N.
本题解析:
本题难度:一般
2、选择题 关于匀速圆周运动的向心力, 下列说法中正确的是
[? ]
A.匀速 圆周运动中向心力是恒力
圆周运动中向心力是恒力
B.匀速圆周运动的向心力是大小不变、方向变化的变力
C.匀速圆周运动的向心力的功率是零
D.匀速圆周运动的向心力一定是物体受到的合力
参考答案:BCD
本题解析:
本题难度:简单
3、选择题 如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=4m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )
A.a处为拉力,方向竖直向上,大小为126N
B.a处为拉力,方向竖直向下,大小为126N
C.b处为拉力,方向竖直向下,大小为6N
D.b处为压力,方向竖直向下,大小为6N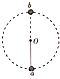
参考答案:A、在最低点,杆子一定表现为拉力,有F-mg=mva2r,则F=mg+mva2r=30+3×160.5N=126N.小球对杆子的作用力方向向下.故A错误,B正确.
? C、在最高点,有mg+F=mvb2r,则F=mvb2r-mg=3×40.5-30N=-6N.所以杆子表现为支持力,球对杆子的作用力方向竖直向下.故C错误,D正确.
故选BD.
本题解析:
本题难度:一般
4、简答题 如图甲所示,一个绝缘倾斜直轨道固定在竖直面内,轨道的AB部分粗糙,BF部分光滑.整个空间存在着竖直方向的周期性变化的匀强电场,电场强度随时间的变化规律如图乙所示,t=0时电场方向竖直向下.在虚线的右侧存在着垂直纸面向里的匀强磁场,磁感应强度为B=
| 2πm q |
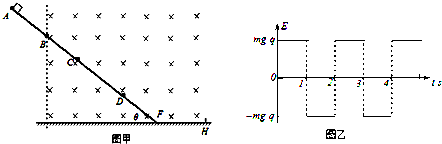
参考答案: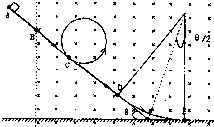
(1)由题意可知?qE=mg?
t=0?到t=1s过程中,对物体有
2mgsinθ-2μmgcosθ=ma?
t=1s到t=2s过程中物体做匀速直线运动,所以
VB=at0=2gsinθ-2μgcosθ?
其中t0=1s
(2)物体在t=2s到t=3s做匀加速直线运动,加速度为
a"=2gsinθ?
在t=3s到t=4s做匀速圆周运动,周期为T=2πmqB=1s
刚好完成一周,在t=4s到t=5s继续以a"做匀加速运动到D点,则
S2-S1=a"t02
解得:sinθ=S2-S12g
(3)物体运动到D点时速度为
VD=VB+a"?2t0=6gsinθ-2μg?cosθ?
离开D点后做匀速圆周运动,半径为R,轨迹如图,则qBVD=mV2DR
由几何关系可知?LR=tanθ2
联立解得L=gπ(3sinθ-μcosθ)tanθ2
答:(1)若轨道倾角为θ,求物块滑动到B的速度大小为2gsinθ-2μgcosθ.
(2)倾角θ的三角函表达式为sinθ=S2-S12g(用S1、S2、g表示);
(3)F点与H点的间距L为gπ(3sinθ-μcosθ)tanθ2.
本题解析:
本题难度:一般
5、选择题 在探究向心力的大小与质量、角速度和半径之间关系的实验中,如图所示,是研究哪两个物理量之间的关系
[? ]
A.研究向心力与质量之间的关系
B.研究向心力与角速度之间的关
C.研究向心力与半径之间的关系
D.研究向心力与线速度之间的关系
参考答案:A
本题解析:
本题难度:一般