时间:2017-07-31 08:12:44
1、简答题 )如图所示,一段闭合螺线管套放在光滑水平玻璃棒上,一个光滑水平玻璃板中心沿螺线管的轴线穿过,板足够长,质量为M的条形磁铁放在板上螺线管管口的一端。现给条形磁铁一个冲量,使条形磁铁以速率v0穿过螺线管,条形磁铁穿出螺线管时的速率为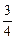 v0,螺线管的质量为
v0,螺线管的质量为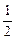 M。
M。
求条形磁铁穿过螺线管的过程中螺线管产生的热量。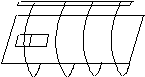
参考答案:Q=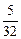 Mv02
Mv02
本题解析:以磁铁和螺线管为系统,系统所受合外力为零,所以系统动量守恒,则:
Mv0=M·(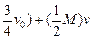 ?①
?①
解得,磁铁穿出螺线管后,螺线管的速度
v=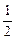 v0
v0
系统相互作用的过程中,系统减少的动能转化为电能,再转化为内能,由能的转化和守恒定律有:
Q=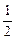 Mv02-
Mv02-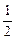 M(
M(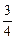 v0)2-
v0)2-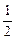 ·(
·(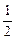 M)v2?②
M)v2?②
将v=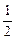 v0代入求得Q=
v0代入求得Q=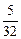 Mv02
Mv02
本题难度:一般
2、选择题 如图所示,在匀强磁场中放置一个电阻不计的平行金属导轨,导轨跟大线圈M相连,导轨上放一根导线ab,磁感线垂直于导轨所在平面,欲使M所包围的小闭合线圈N产生顺时针方方的感应电流,则导线的运动情况可能是(? ).
A.匀速向左运动
B.加速向右运动
C.减速向右运动
D.减速向左运动
参考答案:C
本题解析:本题考查的是电磁感应定律的问题,要使小闭合线圈N产生顺时针方向的感应电流,导线减速向右运动或者加速向左运动;C正确。
本题难度:简单
3、选择题 如图所示,水平放置的平行金属导轨MN和PQ之间接有定值电阻R,导体棒ab长为l且与导轨接触良好,整个装置处于竖直向上的匀强磁场中,现使导体棒ab匀速向右运动,下列说法正确的是( )
A.导体棒ab两端的感应电动势越来越小
B.导体棒ab中的感应电流方向是a→b
C.导体棒ab所受安培力方向水平向右
D.导体棒ab所受合力做功为零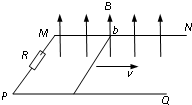
参考答案:A、ab棒切割产生的感应电动势:E=BLv,由于棒匀速运动,v不变,又B、L不变,所以棒ab产生的感应电动势不变.故A错误.
B、根据右手定则得,ab棒中的电流方向从b→a,故B错误.
C、根据左手定则判断知:棒ab所受安培力方向向左,故C错误.
D、棒ab做匀速运动,动能不变,根据动能定理可知合力做功为零,故D正确.
故选:D.
本题解析:
本题难度:简单
4、计算题 电磁炉专用平底锅的锅底均由耐高温的绝缘材料制成.起加热作用的是安在锅底的一系列半径不同的同心导电环.导电环所用材料单位长度的电阻为R0=0.125πΩ/m,从中心向外第n个同心圆环的半径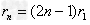 ,(n=1,2,3,…,7),已知r1=1.0cm.当电磁炉开启后,能产生垂直于锅底方向变化的磁场,若已知该磁场的磁感应强度B的变化率为
,(n=1,2,3,…,7),已知r1=1.0cm.当电磁炉开启后,能产生垂直于锅底方向变化的磁场,若已知该磁场的磁感应强度B的变化率为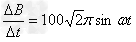 (T/m).求:
(T/m).求:
(1)半径为r1的导电圆环中感应电流的最大值是多少?
(2)假设导电产生的热能全部以波长为1.0×10-6 m的红外线光子辐射出来,那么半径为r1的导电圆环上每分钟辐射出的光子数是多少?
(3)若不计其它损失,所有导电圆环释放的总功率为多大?(以上计算中可取π2=10,普朗克常量h=6.6×10-34 J·s)
参考答案:解:(1)由题意得:
所以电流最大值为:
(2)设半径为r1的导电圆环上每分钟辐射出的光子数是n,则有: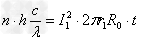 ,其中
,其中 A
A
解得
(3)第n个导电圆环上消耗的电功率为:
所以导电圆环释放的总功率为: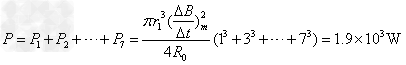
本题解析:
本题难度:一般
5、计算题 如图所示,AB、CD是两根足够长的固定平行金属导轨,两导轨间的距离为L,导轨平面与水平面间的夹角为θ,在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场,磁感应强度为B1,在导轨的AC端连接一个阻值为R的电阻,一根质量为m垂直于导轨放置的金属棒ab,从静止开始沿导轨下滑,已知金属棒ab与导轨间的动摩擦因数为μ,导轨和金属棒的电阻不计。求
(1)此过程中金属棒ab的最大速度?
(2)若金属棒ab下滑到速度最大时,通过的位移为x0,此过程中通过电阻R的电荷量为多少?安培力对金属棒ab所做的功是多大? 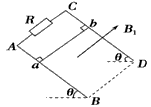
参考答案:解:(1)金属棒ab下滑时因切割磁感线,产生感应电动势,根据法拉第电磁感应定律可得:E=B1Lv
闭合电路中将产生感应电流,根据闭合电路欧姆定律可得:I=E/R
金属棒ab所受的安培力F安方向如图所示,其大小为:F安=B1IL 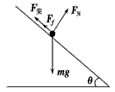
由以上三式可得F安=B12L2v/R
以金属棒ab为研究对象,根据牛顿第二定律有:mgsinθ-μmgcosθ-B12L2v/R=ma
金属棒ab做加速度减小的加速运动,当a=0时速度达到最大值vm
即mgsinθ-μmgcosθ-B12L2vm/R=0
可解得vm=mgR(sinθ-μcosθ)/B12L2
(2)由法拉第电磁感应定律得,平均感应电动势E=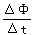 ,平均电流I=
,平均电流I=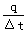 ,通过电阻R的电荷量q=I·Δt=
,通过电阻R的电荷量q=I·Δt=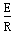 ·Δt=
·Δt=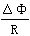 =B1Lx0/R
=B1Lx0/R
金属棒ab下滑过程中重力势能减少Ep=mgx0sinθ,动能增加Ek=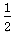 mvm2,摩擦产生的热量Q′=μmgx0cos θ,由能量守恒定律可知
mvm2,摩擦产生的热量Q′=μmgx0cos θ,由能量守恒定律可知
电阻R产生的电热Q=Ep-Ek-Q′,根据功能关系,在金属棒ab下滑过程中克服安培力所做的功等于电路中产生的电能,即安培力所做功的大小
W=mgx0sinθ-μmgx0cosθ-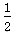 mvm2
mvm2
W=mgx0sinθ-μmgx0cosθ-m3g2R2(sinθ-μcosθ)2/2B14L4
本题解析:
本题难度:困难