1、选择题 一定质量的理想气体从状态A变化到状态B,其变化过程反映在p-T图中是一条直线,如图所示,则此过程中该气体

[? ]
A.体积不变内能增加
B.对外界做功并放出热量
C.不吸热也不放热
D.吸收热量并对外界做功
参考答案:D
本题解析:
本题难度:一般
2、选择题 如图8.1—2所示,A、B 是一定质量的理想气体在两条等温线上的两个状态点,这两点与坐标原点O 和对应坐标轴上的VA、VB坐标所围成的三角形面积分别为SA 、SB,对应温度分别为TA和TB,则(?)

A.SA > SB? TA > TB?
B.SA = SB? TA < TB
C.SA < SB? TA < TB
D.SA > SB? TA < TB
参考答案:C
本题解析:由图可知:三角形的面积等于p与V乘积的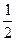 ,
,
∴SA=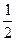 pAVA?SB=
pAVA?SB=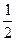 pBVB
pBVB
在A点所在的等温线中,其上各点的pV 乘积相同,因为p与V成反比,所以pAVA=pA VB<pBVB∴SA<SB ?又因为离原点越远,温度越高,所以TA<TB?选C
VB<pBVB∴SA<SB ?又因为离原点越远,温度越高,所以TA<TB?选C
本题难度:简单
3、选择题 如右图,ABCA表示一定质量的理想气体的一个循环过程,下列说法正确的是(?)

A.A→B过程中,气体对外做了功
B.B→C过程中,气体内能增加
C.C→A过程中,气体内能减少
D.C→A过程中,外界对气体做功
参考答案:B
本题解析:
本题难度:简单
4、实验题 用DIS研究一定质量气体在温度不变时,压强与体积关系的实验装置如下图所示,实验步骤如下:
①把注射器活塞移至注射器中间位置,将注射器与压强传感器、数据采集器、计算机逐一连接;
②移动活塞,记录注射器的刻度值V,同时记录对应的由计算机显示的气体压强值p;
③用V-1/p图象处理实验数据,得出如图所示图线。

(1)为了保持封闭气体的质量不变,实验中采取的主要措施是________。
(2)为了保持封闭气体的温度不变,实验中采取的主要措施是______和______。
(3)如果实验操作规范正确,但如图所示的V-1/p图线不过原点,则V0代表________________。
参考答案:(1)在注射器活塞上涂润滑油
(2)移动活塞要缓慢;不能用手握住注射器封闭气体部分
(3)注射器与压强传感器连接部位的气体体积
本题解析:
本题难度:一般
5、填空题 一定质量的气体,在体积不变的条件下,温度由0℃升高到10℃时,其压强的增量为△P1,当它由100℃升高到110℃时,所增加的压强为△P2,则△P1:△P2=___________。
参考答案:1:1
本题解析:
本题难度:简单
微信搜索关注"91考试网"公众号,领30元,获取公务员事业编教师考试资料40G


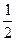 ,
,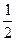 pAVA?SB=
pAVA?SB=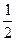 pBVB
pBVB VB<pBVB∴SA<SB ?又因为离原点越远,温度越高,所以TA<TB?选C
VB<pBVB∴SA<SB ?又因为离原点越远,温度越高,所以TA<TB?选C