时间:2017-07-27 13:03:15
1、简答题 某种加速器的理想模型如图1所示:两块相距很近的平行小极板中间各开有一小孔a、b,两极板间电压uab的变化图象如图2所示,电压的最大值为U0、周期为T0,在两极板外有垂直纸面向里的匀强磁场.若将一质量为m0、电荷量为q的带正电的粒子从板内a孔处静止释放,经电场加速后进入磁场,在磁场中运动时间T0后恰能再次从a?孔进入电场加速.现该粒子的质量增加了
| 1 100 |

2、选择题 如图所示,回旋加速器D形盒的半径为R,用来加速质量为m,电量为q的质子,质子每次经过电场区时,都恰好被电压为U的电场加速,且电场可视为匀强电场,使质子由静止加速到能量为E后,由A孔射出 。下列说法正确的是(?)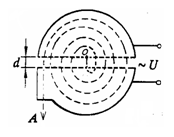 ?
?
A.若加速电压U越高,质子的能量E将越大。
B.若D形盒半径R越大,质子的能量E将越大。
C.若加速电压U越高,质子在加速器中的运动时间将越长。
D.若加速电压U越高,质子在加速器中的运动时间将越短。
3、计算题 质谱仪原理如图所示,a为粒子加速器,电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2,今有一质量为m,电量为+e的电子(不计重力),经加速后,该粒子恰能通过速度选择器,粒子进入分离器后做半径为R的匀速圆周运动.
求:(1)粒子的速度v;
(2)速度选择器的电压U2;
(3)粒子在磁感应强度为B2磁场中做匀速圆周运动的半径R.
4、选择题 1932年,美国的物理学家劳伦斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的两D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的质量为m、电荷量为+q粒子在加速器中被加速,其加速电压恒为U.带电粒子在加速过程中不考虑相对论效应和重力的作用.则( )
A.带电粒子在加速器中第1次和第2次做曲线运动的时间分别为t1和t2,则t1:t2=1:2
B.带电粒子第1次和第2次经过两D形盒间狭缝后轨道半径之比r1:r2=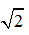 :2
:2
C.两D形盒狭缝间的交变电场的周期T=2πm/qB
D.带电粒子离开回旋加速器时获得的动能为B2q2R2/2m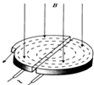
5、选择题 质谱仪的两大重要组成部分是加速电场和偏转磁场,如图所示为质谱仪的原理图,设想有一个静止的质量为m、电荷量为q的带电粒子(不计重力),经电压为U的加速电场加速后垂直进入磁感应强度为B的偏转磁场中,并最终打至底片上的P点。设OP=x,则在下图中,能正确反映x与U之间的函数关系的是( ? )




