时间:2017-07-27 12:49:16
1、计算题 (18分)
如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.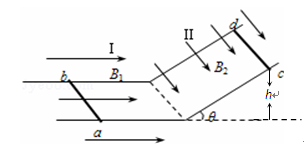
(1)求导体棒cd沿斜轨道下滑的最大速度的大小;
(2)若已知从开始运动到cd棒达到最大速度的过程中,ab棒产生的焦耳热Q=0.45J,求该过程中通过cd棒横截面的电荷量;
(3)若已知cd棒开始运动时距水平轨道高度h=10m,cd棒由静止释放后,为使cd棒中无感应电流,可让磁场Ⅱ的磁感应强度随时间变化,将cd棒开始运动的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0=1T,试求cd棒在倾斜轨道上下滑的这段时间内,磁场Ⅱ的磁感应强度B随时间t变化的关系式.
参考答案:(1)1m/s(2)1C(3)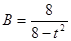 , (t<
, (t<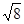 s)
s)
本题解析:(1)在cd从开始运动到达最大速度的过程中ab棒受到的安培力竖直向上,且mg>BIL,故ab棒处于静止状态。
cd棒匀速运动时速度最大,设为vm,棒中感应电动势为E,电流为I,
感应电动势:E=BLvm,电流: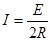 (2分)
(2分)
由平衡条件得:mgsinθ=BIL,代入数据解得:vm=1m/s;(2分)
(2)在cd从开始运动到达最大速度的过程中ab棒受到的安培力竖直向上,且mg>BIL,故ab棒处于静止状态。设cd从开始运动到达最大速度的过程中经过的时间为t,通过的距离为x,cd棒中平均感应电动势为E1,平均电流为I1,通过cd棒横截面的电荷量为q,
由能量守恒定律得:mgxsinθ=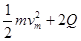 (2分)
(2分)
电动势: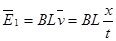 ,电流:
,电流: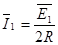 ,
,
电荷量: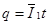 (2分)
(2分)
代入数据解得:q=1C (1分)
(3)设cd棒开始运动时穿过回路的磁通量为Φ0,cd棒在倾斜轨道上下滑的过程中,设加速度大小为a,经过时间t通过的距离为x1,穿过回路的磁通量为Φ,cd棒在倾斜轨道上下滑时间为t0,
则:Φ0=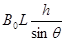 (1分)
(1分)
由牛顿第二定律mgsinθ=ma,则加速度:a=gsinθ,位移:x1=1/2(at2) (2分)
Φ=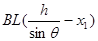 ,
,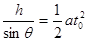 (2分)
(2分)
解得:t0=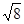 s,
s,
为使cd棒中无感应电流,必须有:Φ0=Φ,(2分)
解得: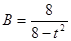 , (t<
, (t<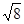 s);(2分)
s);(2分)
考点:能量守恒定律 法拉第电磁感应定律 牛顿第二定律
本题难度:困难
2、计算题 法拉第曾提出一种利用河流发电的设想,并进行了实验研究。实验装置的示意图可用下图表示,两块面积均为S的矩形金属板,平行、正对、竖直地全部浸在河水中,间距为d。水流速度处处相同,大小为v,方向水平。金属板与水流方向平行,地磁场磁感应强度的竖直分量为B,水的电阻率为ρ,水面上方有一阻值为R的电阻通过绝缘导线和电键K连接到两个金属板上。忽略边缘效应,求:
(1)该发电装置的电动势;
(2)通过电阻R的电流强度;
(3)电阻R消耗的电功率。
参考答案:解:(1)由法拉第电磁感应定律,有E=Bdv
(2)两板间河水的电阻
由闭合电路欧姆定律,有
(3)由电功率公式P=I2R
得
本题解析:
本题难度:一般
3、计算题 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距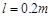 ,电阻
,电阻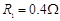 ,导轨上静止放置一质量
,导轨上静止放置一质量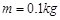 、电阻
、电阻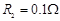 的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度
的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度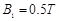 的匀强磁场中,磁场的方向竖直向下,现用一外力
的匀强磁场中,磁场的方向竖直向下,现用一外力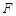 沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求: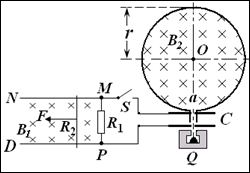
(1)5s末时电阻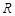 上消耗的电功率;
上消耗的电功率;
(2)5s末时外力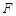 的功率.
的功率.
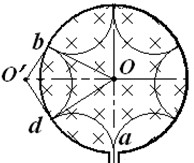
(3)若杆最终以8m/s的速度作匀速运动,此时闭合电键S,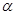 射线源Q释放的
射线源Q释放的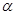 粒子经加速电场C加速后从
粒子经加速电场C加速后从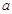 孔对着圆心
孔对着圆心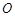 进入半径
进入半径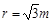 的固定圆筒中(筒壁上的小孔
的固定圆筒中(筒壁上的小孔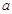 只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为
只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为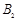 的匀强磁场。
的匀强磁场。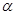 粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从
粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从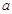 孔背离圆心射出,忽略
孔背离圆心射出,忽略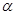 粒子进入加速电场的初速度,若
粒子进入加速电场的初速度,若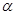 粒子质量
粒子质量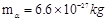 ,电量
,电量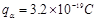 ,则磁感应强度
,则磁感应强度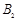 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
参考答案:(1)0.1W(2)0.25W(3)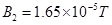 ?
?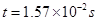
本题解析:(1)5s末杆产生的电动势: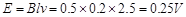 ,
,
电流大小为: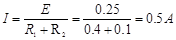
电阻上消耗的电功率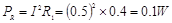
(2)金属棒的加速度: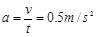 ,由牛顿第二定律可知:
,由牛顿第二定律可知: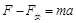
杆受的安培力大小为: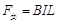
则外力F的功率: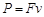
由以上式子可得: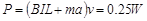
(3)此时回路电流强度为: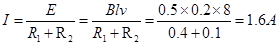
加速电场的电压为: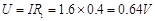
根据动能定理: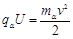
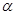 粒子从C孔进入磁场的速度
粒子从C孔进入磁场的速度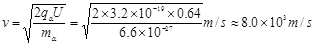
由题意知: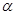 粒子与圆筒壁碰撞5次后从
粒子与圆筒壁碰撞5次后从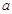 孔离开磁场,由几何关系求得:
孔离开磁场,由几何关系求得: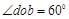 ,轨迹半径
,轨迹半径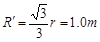 ,又因为:
,又因为: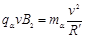
故: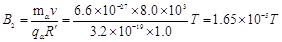
又: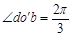 ,粒子作圆周运动转过的圆心角为:
,粒子作圆周运动转过的圆心角为: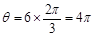
根据: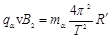 及
及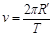
得: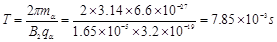 ,粒子在圆筒内运动的总时间:
,粒子在圆筒内运动的总时间: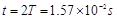 ?
?
点评:本题的综合程度相当高,题目难度大,比较难得全分。其中第一、二两问还比较常见,第三问中,根据所求的进入磁场的速度,利用轨迹可以建立求解的等式。
本题难度:一般
4、选择题 如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且垂直于纸面,MN、PQ为其边界,OO"为其对称轴。一导线折成边长为l的正方形闭合线框abcd,线框在外力作用下由纸面内图示位置从静止开始向右做匀加速运动,若以逆时针方向为电流的正方向,则从线框开始运动到ab边刚进入到PQ右侧磁场的过程中,能反映线框中感应电流随时间变化规律的图像是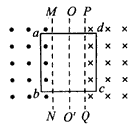
[? ]
A.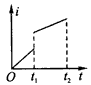
B.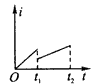
C.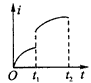
D.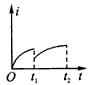
参考答案:B
本题解析:
本题难度:一般
5、选择题 医生做某些特殊手术时,利用电磁血流计来监测通过动脉的血流速度.电磁血流计由一对电极a和b以及磁极N和S构成,磁极间的磁场是均匀的.使用时,两电极a、b均与血管壁接触,两触点的连线、磁场方向和血流速度方向两两垂直,如图所示.由于血液中的正负离子随血流一起在磁场中运动,电极a、b之间会有微小电势差.在达到平衡时,血管内部的电场可看作是匀强电场,血液中的离子所受的电场力和磁场力的合力为零.在某次监测中,两触点的距离为3.0mm,血管壁的厚度可忽略,两触点间的电势差为160?V,磁感应强度的大小为0.040T.则血流速度的近似值和电极a、b的正负为( )
A.1.3m/s,a正、b负
B.2.7m/s,a正、b负
C.1.3m/s,a负、b正
D.2.7m/s,a负、b正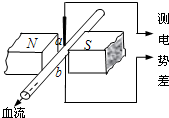
参考答案:血液中正负离子流动时,根据左手定则,正离子受到向上的洛伦兹力,负离子受到向下的洛伦兹力,所以正离子向上偏,负离子向下偏.则a带正电,b带负电.最终血液中的离子所受的电场力和磁场力的合力为零,有qUd=qvB,所以v=UBd=160×10-60.040×3×10-3m/s=1.3m/s.故A正确,B、C、D错误.
故选A.
本题解析:
本题难度:一般