时间:2017-07-27 11:47:33
1、选择题 如图4所示，放置在水平地面上的支架质量为M，支架顶端用细线拴着的摆球质量为m，现将摆球拉至水平位置，而后释放，摆球运动过程中，支架始终不动．以下说法正确的应是（ ）
A．在释放瞬间，支架对地面压力为（m+M）g
B．在释放瞬间，支架对地面压力为Mg
C．摆球到达最低点时，支架对地面压力为（m+M）g
D．摆球到达最低点时，支架对地面压力小于（m+M）g
参考答案：A、释放的瞬间，知细线的拉力为零，则细线对支架误拉力，对支架分析，受重力和支持力，则N=Mg，所以支架对地面的压力为Mg．故A错误，B正确．
C、摆球摆动到最低时，根据动能定理知，mgL=12mv2，根据牛顿第二定律得，F-mg=mv2L=2mg，则F=3mg．则支架对地面的压力为N′=Mg+3mg．故C、D错误．
故选B．
本题解析：
本题难度：简单
2、选择题 如图所示，长为L的轻杆一端固定着质量为m的小球绕另一端O在竖直平面内做圆周运动，则下列说法中正确的是（ ）
A．小球通过最高点时杆受到的弹力不可以为0
B．小球通过最高点时的速度最小值为
| gL |
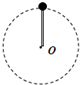
参考答案：A、在最高点，杆子对小球的作用力和小球的重力的合力提供向心力，有F+mg=mv2L，当v=
本题解析：
本题难度：简单
3、简答题 在“用圆锥摆实验验证向心力公式“的实验中，AB为竖直转轴，细绳一端系在A点，另一端与小球C相连，如图所示．当转轴转动时，C球在水平面内做匀速圆周运动．实验步骤如下：
①测量AC间细绳长度l；
②使AB轴转动，并带动C球在水平面内做匀速圆周运动；
③测出此时C球做匀速圆周运动的周期T，并标出C球球心在AB轴上的投影点D，测出AD间距为S；
④算出C球做匀速圆周运动所需的向心力F；
⑤算出C球所受的合力F；
⑥验证向心力公式．
（I?）在上述实验中还需要测量的物理量有哪些______
A．C球的直径?B．C球的质量?C．C球转动的角速度?D．当地的重力加速度g
（II）为了验证向心力公式正确．请用已知的物理量和第（I）题中你所选择的物理量表示出AD间距S=______．
（III）这一实验方法简单易行．但是有几个因素可能会影响实验的成功，请写出一条：______．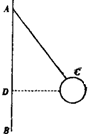
参考答案：（1）该实验的原理是根据几何关系求出指向圆心的合力，再根据向心力公式求出向心力的值，看两者是否相等，所以还要知道小球的直径及当地的重力加速度g；
故选AD
（?2?）根据圆锥摆的周期公式得：T=2π
本题解析：
本题难度：一般
4、计算题 如图所示，细绳一端系着质量为M＝0.6 kg的物体，静止在水平盘面上，另一端通过光滑小孔吊着质量m＝0.3 kg的物体，M的中心与小孔距离为0.2 m，并知M和水平盘面的最大静摩擦力为2 N．现使此水平盘绕中心轴转动，问角速度ω在什么范围内m处于静止状态？(g取10 m/s2)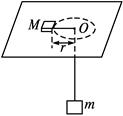
参考答案：2.9 rad/s≤ω≤6.5 rad/s
本题解析：设物体M和水平盘面保持相对静止，当ω具有最小值时，M有向着圆心O运动的趋势，故水平盘面对M的摩擦力方向背向圆心，且等于最大静摩擦力fmax＝2 N.
对于M：F－fmax＝Mrω
，则ω1＝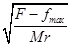
＝ 
＝ 
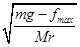
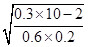rad/s≈2.9 rad/s.
当ω具有最大值时，M有离开圆心O的趋势，
水平盘面对M摩擦力的方向指向圆心，fmax＝2 N.
对M有：F＋fmax＝Mrω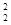
则ω2＝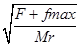
＝
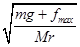≈6.5 rad/s，
故ω的范围是2.9 rad/s≤ω≤6.5 rad/s.
本题难度：一般
5、计算题 如图所示，水平长杆AB绕过B端的竖直轴OO"匀速转动，在杆上套有一个质量m=1kg的圆环，若圆环与水 平杆间的动摩擦因数μ=0.5，且假设最大静摩擦力与滑动摩擦力大小相等，则：
(1)当杆的转动角速度ω=2 rad/s时，圆环的最大回转半径为多大？
(2)如果水平杆的转动角速度降为ω"=1.5 rad/s，圆环能否相对于杆静止在原位置，此时它所受到的摩擦力有多大？(g 取10 m/s2） 
参考答案：解：
(1)圆环在水平面内做匀速圆周运动的向心力是杆施加给它的摩擦力提供的，则最大向心力F向=μmg，代入公式F向= mRmaxω2，得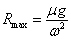
．代入数据可得Rmax=1.25 m．
(2)当水平杆的转动角速度降为1.5 rad/s时，圆环所需的向心力减小，则圆环所受的静摩擦力随之减小，不会相对于杆滑动，故圆环相对杆仍静止在原来的位置，此时的静摩擦力f= mRmaxω"2=2.81 N．
本题解析：
本题难度：一般