时间:2017-07-27 11:43:26
1、计算题 甲、乙两车,从同一处,同时开始作同向直线运动。已知甲车以14m/s 的速度作匀速直线运动,乙车从静止开始作匀加速运动,加速度为2 m/s2。试分析:
(1)经过多长时间,乙车追上甲车?此时乙车的速度多大?
(2)经过多长时间,乙车落后于甲车的距离最大?落后的最大距离是多少?
参考答案:(1)14s,28m/s
(2)7s,49m
本题解析:
本题难度:困难
2、选择题 一质点沿直线Ox方向做减速直线运动,它离开O点的距离x随时间变化的关系为x=6t-2t3(m),它的速度v随时间t变化的关系为v=6-6t2(m/s),则该质点在t=2s时的瞬时速度、从t=0到t=2s间的平均速度、平均速率分别为( )
A.-18m/s、-2m/s、6m/s
B.-18m/s、-2m/s、2m/s
C.-2m/s、-2m/s、-18m/s
D.-18m/s、6m/s、6m/s
参考答案:该质点在t=2s时的瞬时速度为 v=6-6t2(m/s)=6-6×22=-18m/s;
据题意,质点离开O点的距离x随时间变化的关系为 x=6t-2t3(m),可得:
t=0时,x=0m;
t=2s时,x′=-4m;
故2s内位移为:△x=x′-x=-4m-0m=-4m;
2s内的平均速度为:.v=△xt=-42m/s=-2m/s
当v=0时,由v=6-6t2(m/s)得,t=1s,此时 x1=6t-2t3(m)=4m,在前1s内质点通过的路程为 S1=x1=4m;
在后1s内通过的路程是 S2=2|x1|+|x′|=2×4+4=12m;
则平均速率 .v速率=S1+S2t=122=6m/s
故选:A
本题解析:
本题难度:简单
3、选择题 一辆汽车运动的位移时间关系式为x=8t-2t2(m/s),则( )
A.这个汽车做匀减速运动
B.这个汽车的初速度为8m/s
C.这个汽车的加速度为-2m/s2
D.两秒后汽车停下
参考答案:根据x=v0t+12at2=8t-2t2,v0=8m/s,a=-4m/s2.根据速度时间公式v=v0+at,当v=0时,t=2s.故A、B、D正确,C错误.
故选ABD.
本题解析:
本题难度:一般
4、简答题 某物体在一条直线上从A点运动到B点,又从B点运动到A点,两次运动的起始点分别作为两次位移的0点和计时的起点,两次观测得的数据如下,试分析物体两次做何种运动.
| 物体运动 起始点 | 所测 物理量 | 测?量?次?数 | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| A (v0=0) | 时刻t/s | 0.55 | 1.09 | 1.67 | 2.23 | 2.74 |
| 位移s/m | 0.2511 | 0.5052 | 0.7493 | 1.0014 | 1.2547 | |
| B (v0=0) | 时刻t/s | 0.89 | 1.24 | 1.52 | 1.76 | 1.97 |
| 位移s/m | 0.2545 | 0.5009 | 0.7450 | 1.0036 | 1.2549 | |
参考答案:物体从A到B的运动为匀速直线运动,从B运动到A是作匀变速运动。
本题解析:作出物体从A运动到B的过程中的位移-时间图象,如图3所示: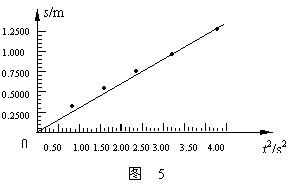
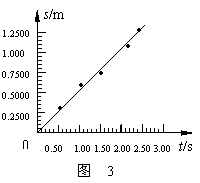
从图3所示的s-t图线中,可以得到:在误差允许的范围内,物体从A到B的运动为匀速直线运动.
作出物体从B运动到A的过程位移-时间图象,如图4所示。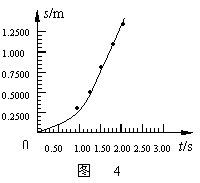
从图中可以断定物体从B到A不是作匀速直线运动。从图线的形态猜想图线可能是一条抛物线,即物体可能作匀变速直线运动,为确定是否为匀变速直线运动,作s-t2图象如图5所示,从
图5可知,物体从B运动到A是作匀变速运动。
本题难度:简单
5、简答题 小韩住在高层楼房,现乘电梯从家里到一楼地面,如图记录的是电梯速度随时间变化的关系.请问:
(1)由图可知,电梯下楼过程中各时间段分别做什么运动?
(2)小韩所住的楼层距地面的高度是多少?
(3)电梯在0~2s与5~8s内的加速度大小之比是多少?
参考答案:(1)由图可知物体在0-2s匀加速下降,2-5s匀速下降,5-8s匀减速下降.
(2)电梯下降的高度等于图象与时间轴围成的面积,故小韩所住的楼层距地面的高度:h=(3+82)×5m=27.5m
(3)重物在0~2s内的加速度a1=△v△t=5-02m/s2=2.5m/s2,重物在5~8s内的加速度a2=△v△t=0-58-5m/s2=-53m/s2,
所以两段时间内的加速度大小之比为a1:a2=3:2.
答:(1)物体在0-2s匀加速下降,2-5s匀速下降,5-8s匀减速下降.(2)楼层离地面的高度为27m; (3)加速度之比为3:2.
本题解析:
本题难度:一般