时间:2017-07-27 11:34:35
1、计算题 如图所示，三个可视为质点的物块A，B，C，在水平面上排成一条直线，且彼此间隔一定距离。已知mA=mB=10 kg，mC=20 kg，C的左侧水平面光滑，C的右侧水平面粗糙，A，B与粗糙水平面间的动摩擦因数μA =μB=0.4，C与粗糙水平面间动摩擦因数μC=0.2，A具有20 J的初动能向右运动，与静止的B发生碰撞后粘在一起，又与静止的C发生碰撞，最后A，B，C粘成一个整体，求：（取g=10 m/s2）
（1）在第二次碰撞中损失的机械能有多少？
（2）这个整体在粗糙的水平面上滑行的距离是多少？ 
参考答案：解：（1）由于A的初动能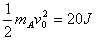
得A的初速度v0=2 m/s
A，B发生完全非弹性碰撞，根据动量守恒定律
mAv0=(mA+mB)v1，得v1=1 m/s
A，B与C发生完全非弹性碰撞，根据动量守恒定律
(mA+mB)v1=(mA+mB+mC)v2，得v2=0.5 m/s
在第二次碰撞中损失的机械能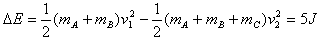
（2）A，B，C整体在粗糙水平面上所受的摩擦力f=fA+fB+fC=μAmAg+μBmBg+μCmCg=120 N
根据动能定理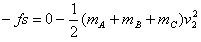
解得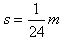
本题解析：
本题难度：困难
2、选择题 如图所示，两个物体1和2置于光滑的水平面上，它们的质量分别为m1和m2，且m1＜m2，现将两个大小 均为F、方向相反的恒力同时作用在1和2上，经相同的距离后（两物体还没接触），撤去两个力，此后两物体碰撞并粘在一起，碰撞后，两物体将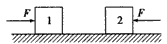
[? ]
A．向左运动
B．向右运动
C．停止运动
D．运动，但方向不能确定
参考答案：A
本题解析：
本题难度：一般
3、计算题 质量分别为m1和m2的两个小球在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞，碰后m2被右侧的墙原速弹回，又与m1相碰，碰后两球都静止，求：第一次碰后m1球的速度。
参考答案：解：根据动量守恒定律得
解得
本题解析：
本题难度：一般
4、计算题 光滑的水平面上，质量为m1的小球甲以速率v0向右运动。在小球甲的前方A点处有一质量为m2的小球乙处于静止状态，如图所示。甲与乙发生正碰后均向右运动。乙被墙壁C弹回后与甲在B点相遇，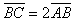
。已知小球间的碰撞及小球与墙壁之间的碰撞均无机械能损失，求求甲、乙两球的质量之比
。 
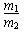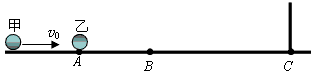
参考答案：解：两球发生弹性碰撞，设碰后甲、乙两球的速度分别为v1、v2，则
m1v0=m1v1+m2v2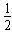
m1v02=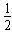m1v1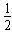2+m2v22
从两球碰撞后到它们再次相遇，甲和乙的速度大小保持不变，由于BC=2AB，则甲和乙通过的路程之比为v1:v2=1:5
联立解得
本题解析：
本题难度：一般
5、选择题 质量相等的A、B两球在光滑水平面上沿同一直线、同一方向运动，A球的动量是7kg·m/s，B球的动量是5 kg·m/s，当A球追上B球发生碰撞，则碰撞后A、B两球的动量可能值是
[? ]
A.pA"=6 kg·m/s，pB"=6 kg·m/s
B.pA"=3 kg·m/s，pB"=9 kg·m/s
C.pA"=-2 kg·m/s，pB"=14 kg·m/s
D.pA"=-4 kg·m/s，pB"=17 kg·m/s
参考答案：A
本题解析：
本题难度：一般