时间:2017-07-17 08:13:05
1、选择题 如图所示,小球由细线AB、AC拉住静止,AB保持水平,AC与竖直方向成α角,此时AC对球的拉力为T1。现将AB线烧断,烧断瞬间,AC对小球拉力为T2,则T1与T2之比为( )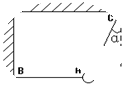
A.1∶1 B.1∶cos2α C.cos2α∶1 D.sin2α∶cos2α
参考答案:B
本题解析:烧断之前,小球在三个力的作用下平衡,则绳子AC 上的弹力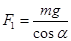 。烧断之后的瞬间,小球即将做圆周运动,此刻速度为零,所以向心力为
。烧断之后的瞬间,小球即将做圆周运动,此刻速度为零,所以向心力为 ,两种情况下,绳子AC上的拉力之比为
,两种情况下,绳子AC上的拉力之比为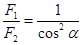 ,选项B正确。
,选项B正确。
考点:本题考查力的平衡和圆周运动的向心力。
本题难度:一般
2、计算题 一质量为m1=1 kg、带电量为q=0.5 C的小球M以速度v=4.5 m/s自光滑平台右端水平飞出,不计空气阻力,小球M飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,圆轨道ABC的形状为半径R<4 m的圆截去了左上角127°的圆弧,CB为其竖直直径,在过A点的竖直线OO′的右边空间存在竖直向下的匀强电场,电场强度大小为E=10 V/m.(sin53°=0.8,cos53°=0.6,重力加速度g取10 m/s2)求: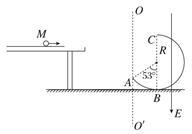
(1)小球M经过A点的速度大小vA;
(2)欲使小球M在圆轨道运动时不脱离圆轨道,求半径R的取值应满足什么条件?
参考答案:(1) (2)0<R≤
(2)0<R≤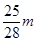 或
或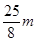 ≤R<4 m
≤R<4 m
本题解析:(1)小球M飞离平台后做平抛运动,故有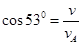 ,解得
,解得
(2)(i)小球M由A点沿切线落入竖直光滑圆轨道ABC后,小球M沿着轨道做圆周运动,
若恰能滑过圆的最高点C,设滑至最高点的速度为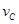 ,临界条件为
,临界条件为
根据动能定理有:
联立可得: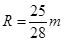
故当 时,小球M沿着轨道做圆周运动,且能从圆的最高点C飞出
时,小球M沿着轨道做圆周运动,且能从圆的最高点C飞出
(
本题难度:困难
3、选择题 铁路在弯道处的内外轨道高低是不同的,已知内外轨道水平面倾角为θ(图),弯道处的圆弧半径为R,若质量为m的火车转弯时速度小于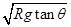 ,则(? )
,则(? )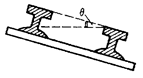
A.内轨对内侧车轮轮缘有挤压;
B.外轨对外侧车轮轮缘有挤压;
C.这时铁轨对火车的支持力等于mg/cosθ;
D.这时铁轨对火车的支持力大于mg/cosθ.
参考答案:A
本题解析:对火车受力分析:重力mg和轨道的支持力N,当火车恰好对轨道无压力时,由牛顿第二定律可得: ?
?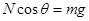 ,联立解得:
,联立解得: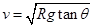 .当火车的速度
.当火车的速度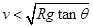 时,火车对内轨产生压力,故选项A正确B错误;又因为火车在竖直方向上静止且同时拐弯需要向心力,故支持力大于重力,即选项CD错误.
时,火车对内轨产生压力,故选项A正确B错误;又因为火车在竖直方向上静止且同时拐弯需要向心力,故支持力大于重力,即选项CD错误.
本题难度:一般
4、计算题 飞机在竖直平面内做半径为400m的匀速圆周运动,其速度是150m/s,飞行员质量为80kg,g取10m/s2.求:
(1)飞机在轨道最低点飞行员头朝上时,飞行员对座椅的压力大小和方向。
(2)飞机在轨道最高点飞机员头朝下时,飞行员对座椅的压力大小和方向。
参考答案:(1)5300N,方向垂直座椅向下(2)大小3700N,方向垂直座椅向上
本题解析:(1)最低点:分析飞行员受力: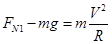 ?
? 方向垂直座椅向上………………………………(4分)
方向垂直座椅向上………………………………(4分)
由牛顿第三定律,飞行员对座椅压力大小5300N,方向垂直座椅向下。………………(1分)
(2)最高点:飞行员受力: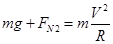 ?
? 方向垂直座椅向下……………………………………(4分)
方向垂直座椅向下……………………………………(4分)
由牛顿第三定律,飞行员对座椅压力大小3700N,方向垂直座椅向上。………………(1分)
本题难度:简单
5、选择题 关于匀速圆周运动, 下列认识正确的是
[? ]
A. 匀速圆周运动是匀速运动
B. 匀速圆周运动是变速运动
C. 匀速圆周运动的线速度不变
D. 匀速圆周运动的周期不变
参考答案:BD
本题解析:
本题难度:简单