时间:2017-07-17 08:08:28
1、填空题 已知氕(11H)、氘(12H)、氚(13H)三个带电粒子,它们以相同的速度垂直射入同一匀强磁场中,做匀速圆周运动.则半径最大的是______,周期最长的是______.
参考答案:当洛伦兹力提供向心力做匀速圆周运动,则有Bqv=mv2R
得:R=mvBq?由于带电粒子们的B、q、v均相同,所以R与m成正比.
而氕(11H)、氘(12H)、氚(13H)三个带电粒子中质量最大则是氚(13H),所以半径最大的是氚(13H);
由周期公式得:T=2πmBq? 由于带电粒子们的B、q均相同,所以T与m成正比.
而氕(11H)、氘(12H)、氚(13H)三个带电粒子中质量最大则是氚(13H),所以周期最长的是氚(13H);
故答案为:氚(13H);氚(13H)
本题解析:
本题难度:一般
2、计算题 (16分)某装置用磁场控制带电粒子的运动,工作原理如图所示。装置的长为 L,上下两个相同的矩形区域内存在匀强磁场,磁感应强度大小均为B、方向与纸面垂直且相反,两磁场的间距为d。装置右端有一收集板,M、N、P为板上的三点,M位于轴线OO′上,N、P分别位于下方磁场的上、下边界上。在纸面内,质量为m、电荷量为-q的粒子以某一速度从装置左端的中点射入,方向与轴线成30°角,经过上方的磁场区域一次,恰好到达P点。改变粒子入射速度的大小,可以控制粒子到达收集板上的位置。不计粒子的重力。
(1)求磁场区域的宽度h;
(2)欲使粒子到达收集板的位置从P点移到N点,求粒子入射速度的最小变化量Δv;
(3)欲使粒子到达M点,求粒子入射速度大小的可能值。
参考答案:(1)h=(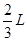 -
- )(1-
)(1-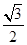 );(2)Δv=
);(2)Δv=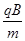 (
(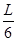 -
- );(3)vn=
);(3)vn=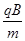 (
(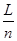 -
- )(2≤n<
)(2≤n<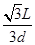 ,n取整数)
,n取整数)
本题解析:(1)设带电粒子在磁场中运动的轨道半径为r,依题意作出带电粒子的运动轨迹如下图所示。
由图中几何关系有:L=3rsin30°+ ,h=r(1-cos30°)
,h=r(1-cos30°)
解得:h=(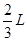 -
- )(1-
)(1-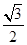 )
)
(2)设带电粒子初始入射速度为v1,改变速度后仍然经过上方的磁场区域一次后到达N点,此时速度的改变量最小,设为v2,粒子改变速度后,在磁场中运动的轨道半径为r′,带电粒子的运动轨迹如下图所示。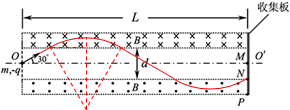
由图中几何关系有:L=4r′sin30°+
根据牛顿第二定律和洛伦兹力大小公式有:qv1B=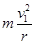 ,qv2B=
,qv2B=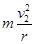
粒子入射速度的最小变化量Δv=|v2-v1|
联立以上各式解得:Δv=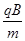 (
(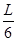 -
- )
)
(3)粒子可能从上方磁场出来后经过M点,也可能从下方磁场出来后经过M点,不妨假设粒子共n次经过了磁场区域到达了M点,此时在磁场中运动的轨道半径为rn,速度为vn,根据牛顿第二定律和洛伦兹力大小公式有:qvnB=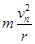
根据几何关系有:L=2nrnsin30°+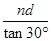
解得:vn=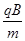 (
(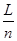 -
- )
)
由于粒子经过上方的磁场区域一次,恰好到达P点,因此粒子不可能只经过上方一次射出后直接到达M点,因此有:n≥2
又因为,粒子必须能够经过磁场改变其运动速度的方向才能到达M点,因此满足n<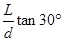 =
=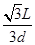
所以:vn=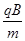 (
(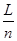 -
- )(其中2≤n<
)(其中2≤n<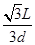 ,且n为整数)
,且n为整数)
本题难度:困难
3、选择题 如图所示,水平放置的平行板电容器间有垂直纸面向里的匀强磁场,开关S闭合时一带电粒子恰好水平向右匀速穿过两板,重力不计。对相同状态入射的粒子,下列说法正确的是 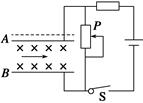
A.保持开关闭合,若滑片P向上滑动,粒子不可能从极板边缘射出
B.保持开关闭合,若滑片P向下滑动,粒子不可能从极板边缘射出
C.保持开关闭合,若A极板向上移动后,调节滑片P的位置,粒子仍可能沿直线射出
D.如果开关断开,粒子继续沿直线射出
参考答案:C
本题解析:带电粒子水平向右匀速穿过两板时,电场力与洛伦兹力平衡.保持开关闭合,若滑片P向上滑动,变阻器接入电路的电阻减小,变阻器两端的电压减小,电容器板间电压减小,板间场强减小,带电粒子所受的电场力减小,若粒子带负电,电场力向上,洛伦兹力向下,洛伦兹力大于电场力,则粒子将向下偏转,可从下极板边缘射出,故A错误;保持开关闭合,若滑片P向下滑动,板间电压增大,由 可知,板间场强增大,若粒子带正电,则粒子所受电场力向下,洛仑兹力向上,带电粒子受电场力增大,则粒子将向下偏转,能从下极板边缘射出,故B错误;保持开关闭合,若只将A极板向上移动后,板间距离增大,这时若将滑片向下滑增大板间电压,由
可知,板间场强增大,若粒子带正电,则粒子所受电场力向下,洛仑兹力向上,带电粒子受电场力增大,则粒子将向下偏转,能从下极板边缘射出,故B错误;保持开关闭合,若只将A极板向上移动后,板间距离增大,这时若将滑片向下滑增大板间电压,由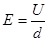 场强可保持不变,带电粒子所受的电场不变,与洛伦兹力仍相等,可以沿直线运动,故C正确;若开关断开,则电容器与电源断开,而与变阻器形成通路,电容器将通过变阻器放电,电荷量不断减小,板间电压不断减小,由
场强可保持不变,带电粒子所受的电场不变,与洛伦兹力仍相等,可以沿直线运动,故C正确;若开关断开,则电容器与电源断开,而与变阻器形成通路,电容器将通过变阻器放电,电荷量不断减小,板间电压不断减小,由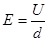 两板间的电场强度要减小,故所受电场力减小,粒子不会做直线运动,故D错误。
两板间的电场强度要减小,故所受电场力减小,粒子不会做直线运动,故D错误。
考点:带电粒子在复合场中的运动;恒定电流。
本题难度:一般
4、计算题 如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿y轴负方向的匀强电场;第四象限无电场和磁场。现有一质量为m、电荷量为q的粒子以速度v0从y轴上的M点沿x轴负方向进入电场,不计粒子的重力,粒子经x轴上的N点和P点最后又回到M点,设OM=L,ON=2L。求:
(1)电场强度E的大小;
(2)匀强磁场的磁感应强度的大小和方向;
(3)粒子从M点进入电场经N、P点最后又回到M点所用的时间。
参考答案:解:(1)粒子从M至N运动过程为类平抛运动,设运动时间为t1,根据运动的分解有:
x方向: ?①
?①
y方向: ?②
?② ?③
?③
联解①②③得: ?④
?④
(2)设粒子在N点时的速度vN与x轴成θ角,则由运动的合成与分解有: ?⑤
?⑤ ⑥
⑥
设带电粒子在磁场中做匀速圆周运动的半径为R,圆心在O′处,过P点的速度方向与x夹角为θ′,作出轨迹如图所示。则由几何关系有: ⑦
⑦ ⑧
⑧ ⑨
⑨
由牛顿第二定律有: ⑩
⑩
联解⑤⑥⑦⑧⑨⑩得: ,方向垂直纸面向里 ⑾
,方向垂直纸面向里 ⑾
(3)粒子从M至N为类平抛运动,时间为t1;在磁场中做匀速圆周运动,时间为t2;从P至M做匀速直线运动,时间为t3。 www.91exAm.org则有: ?⑿
?⑿ ?⒀
?⒀ ?⒁
?⒁ ?⒂
?⒂
联解①⑾⑿⒀⒁⒂得: ⒃
⒃
本题解析:
本题难度:困难
5、计算题 (9分)如图所示,匀强磁场宽L=30cm,B=3.34×10-3?T,方向垂直纸面向里,设一质子以v0=1.6×105?m/s的速度垂直于磁场B的方向从小孔C射入磁场,然后打到照相底片上的A点,质子的质量为1.67×10-27?kg;质子的电量为1.6×10-19?C.求: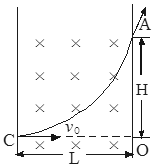
(1)质子在磁场中运动的轨道半径r;
(2)A点距入射线方向上的O点的距离H;
(3)质子从C孔射入到A点所需的时间t.(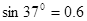 ,结果保留1位有效数字)
,结果保留1位有效数字)
参考答案:(1)0.5m;(2)0.1m;(3)2×10-6 s。
本题解析:(1)由洛伦兹力提供向心力,则:Bqv=m ? 3分
? 3分
r=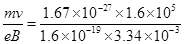 m="0.5" m? 1分
m="0.5" m? 1分
(2)由平面几何知识得:r2=L2+(r-H)2?得H="0.1" m? 2分
(3)由几何知识得质子在磁场中转动的角度为37°,则运动的时间为:
t= ×37°=
×37°=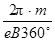 ×37°=2×10-6 s? 3分
×37°=2×10-6 s? 3分
本题难度:一般