时间:2017-07-17 07:40:38
1、选择题 重为100N长1m的质量分布不均匀铁棒平放在水平面上，某人将它一端缓慢竖起，需做功55J，若将它另一端缓慢竖起，需做功(? )
A．45J
B．55J
C．60J
D．65J
参考答案：A
本题解析：因铁棒质量分布不均匀，重心不在中点，由W=mgh得，重心离地面为h=W/mg=55/100=0.55m，若将它另一端缓慢竖起，则做功为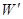
=mg（1m-h）=100
J，A对。
本题难度：简单
2、简答题 如图所示为研究某种弹射装置的示意图，光滑的水平导轨MN右端N处与水平传送带理想连接，传送带足够长，皮带轮沿逆时针方向转动，带动皮带以恒定速度v=2.0m/s匀速传动．三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上，开始时在B、C间有一压缩的轻弹簧，两滑块用细绳相连处于静止状态．滑块A以初速度v0=4.0m/s沿B、C连线方向向B运动，A与B碰撞后粘合在一起，碰撞时间极短，可认为A与B碰撞过程中滑块C的速度仍为零．因碰撞使连接B、C的细绳受扰动而突然断开，弹簧伸展，从而使C与A、B分离．滑块C脱离弹簧后以速度vC=4.0m/s滑上传送带．已知滑块C与传送带间的动摩擦因数μ=0.20，重力加速度g取10m/s2．
（1）求滑块C在传送带上向右滑动距N点的最远距离sm；
（2）求弹簧锁定时的弹性势能Ep；
（3）求滑块C在传送带上运动的整个过程中与传送带之间因摩擦产生的内能Q．
参考答案：（1）滑块C滑上传送带做匀减速运动，当速度减为零时，滑动的距离最远．
由动能定理?-μmgsm=0-12mv2C
解得sm=4.0?m
（2）设A、B碰撞后的速度为v1，A、B与C分离时的速度为v2，由动量守恒定律
mv0=2mv1
2mv1=2mv2+mvC
解得v1=12v0，v2=0
由能量守恒定律
Ep+12×2mv12=12×2mv22+12mvC2
解得Ep=4.0?J
（3）滑块在传送带上向右匀减速运动，设滑块C在传送带上运动的加速度为a，滑块速度减为零的时间为t1，向右的位移为s1，在同样时间内传送带向左的位移为x1，根据牛顿第二定律和运动学公式
a=μmgm=2m/s2．
滑块C速度减小到零所需的时间t1=vca=2s．
滑块的位移s1=vc22a=164m=4m．
传送带的位移x1=vt1=2×2m=4m，
相对路程△x1=s1+x1=8m．
然后滑块返回做匀加速直线运动，当速度达到传送带速度一起做匀速直线运动．
匀加速直线运动的时间t2=va=22s=1s，
滑块C的位移s2=12at22=12×2×1m=1m．
传送带的位移x2=vt2=2m
相对路程△x2=x2-s2=1m．
则摩擦产生的内能Q=μmg（△x1+△x2）=0.2×10×9J=18J．
答：（1）滑块C在传送带上向右滑动距N点的最远距离为4.0m．
（2）弹簧锁定时的弹性势能为4.0J．
（3）滑块C在传送带上运动的整个过程中与传送带之间因摩擦产生的内能为4.0J．
本题解析：
本题难度：一般
3、计算题 倾角为30°的足够长光滑斜面下端与一足够长光滑水平面相接,连接处用一光滑小圆弧过渡,斜面上距水平面高度分别为h1="5" m和h2="0.2" m的两点上,各固定一小球A和B.某时刻由静止开始释放A球,经过一段时间t后,同样由静止开始释放B球.g取10? m/s2,则: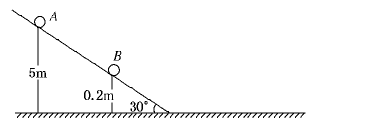
(1)为了保证A、B两球不会在斜面上相碰,t最长不能超过多少?
(2)在满足(1)的情况下,为了保证两球在水平面上的碰撞次数不少于两次,两球的质量mA和mB应满足什么条件?(假设两球的碰撞过程没有能量损失)
参考答案：(1) 1.6 s(2)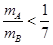 
本题解析：(1)设两球在斜面上下滑的加速度为a,根据牛顿第二定律得:
mgsin30°=ma
设A?B两球下滑到斜面底端所用时间分别为t1和t2,则:
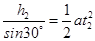
所以:t=t1-t2="1.6" s.
(2)设A?B两球下滑到斜面底端时速度分别为v1和v2,第一次相碰后速度分别为vA和vB,则根据机械能守恒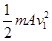
=mAgh1①
=mBgh2②
根据动量守恒和能量守恒
mAv1+mBv2=mAvA+mBvB③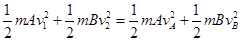
④
为使两球能发生第二次碰撞,应满足
vA<0且|vA|>vB⑤
由①②③④⑤代入数据后可得:.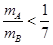
本题难度：一般
4、简答题 如图所示，在纸平面内建立的直角坐标系xoy，在第一象限的区域存在沿y轴正方向的匀强电场．现有一质量为m，电量为e的电子从第一象限的某点P（L，
8 |
| L 4 |
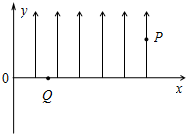
参考答案：（1）电子做类似平抛运动，有：
3L4=v0t
本题解析：
本题难度：一般
5、简答题 如图所示，足够长的水平粗糙轨道与固定在水平面上的光滑弧形轨道在P点相切，质量为m的滑块B静止于P点；质量为2m的滑块A由静止开始沿着光滑弧形轨道下滑，下滑的起始位置距水平轨道的高度为h，滑块A在P点与静止的滑块B碰撞后，两滑块粘合在一起共同向左运动．两滑块均可视为质点，且与水平轨道的动摩擦因素均为μ，P点切线水平．求：
（1）滑块A到达P点与B碰前瞬间的速度大小；
（2）两滑块最终停止时距P点的距离．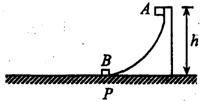
参考答案：
（1）设滑块A到达P点与B碰前瞬间的速度为v0，由机械能守恒定律有：
2mgh=12?2mν20
解得ν0=
本题解析：
本题难度：一般