时间:2017-07-10 21:31:52
1、计算题 如图所示,两木块的质量为m、M,中间弹簧的劲度系数为k,弹簧下端与M连接,m与弹簧不连接,现将m下压一段距离释放,它就上下做简谐运动,振动过程中,m始终没有离开弹簧.试求:
(1)m振动的振幅的最大值.
(2)m以最大振幅振动时,M对地面的最大压力.
参考答案:解:(1)在平衡位置时,弹簧的压缩量为x0,有kx0=mg
要使m振动过程中不离开弹簧,m振动的最高点不能高于弹簧原长处,所以m振动的振幅的最大值A=x0=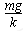
(2)m以最大振幅A振动时,振动到最低点,弹簧的压缩量最大,为2A=2x0=
对M受力分析可得:N=Mg+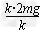 =Mg+2mg
=Mg+2mg
由牛顿第三定律得,M对地面的最大压力为Mg+2mg
本题解析:
本题难度:一般
2、选择题 某质点以大小为0.8m/s2的加速度做初速度为零的匀加速直线运动,则
A.在任意一秒内速度的变化大小都是0.8m/s
B.在任意一秒内,末速度一定等于初速度的0.8倍
C.在任意一秒内,初速度一定比前一秒末的速度增加0.8m/s
D.第1s内、第2s内、第3s内的位移之比为1:3:5
参考答案:AD
本题解析:分析:做匀加速直线运动的物体的加速度为0.8m/s2,知在任意1s内的末速度比初速度大0.8m/s.
解答:A、B、质点以大小为0.8m/s2的加速度做初速度为零的匀加速直线运动,故任意一秒内速度的变化大小都是0.8m/s,故A正确,B错误;
C、在任意一秒内,初速度一定与前一秒末的速度是同一个时刻的速度,一定相同,故C错误;
D、质点以大小为0.8m/s2的加速度做初速度为零的匀加速直线运动,根据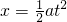 ,前1s、前2s、前3s的位移之比为1:4:9,故第一秒、第二秒、第三秒的位移之比为1:3:5,故D正确;
,前1s、前2s、前3s的位移之比为1:4:9,故第一秒、第二秒、第三秒的位移之比为1:3:5,故D正确;
故选AD.
点评:解决本题的关键知道做匀加速直线运动的物体的加速度为0.8m/s2,在任意1s内的末速度比初速度大0.8m/s.
本题难度:困难
3、填空题 在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为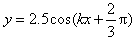 (单位:m),式中k=1 m-1。将一光滑小环套在该金属杆上,并从x=0处以v0=5 m/s的初速度沿杆向下运动,取重力加速度g=10 m/s2。则当小环运动到
(单位:m),式中k=1 m-1。将一光滑小环套在该金属杆上,并从x=0处以v0=5 m/s的初速度沿杆向下运动,取重力加速度g=10 m/s2。则当小环运动到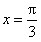 m时的速度大小v=_____m/s;该小环在x轴方向最远能运动到x=____m处。
m时的速度大小v=_____m/s;该小环在x轴方向最远能运动到x=____m处。 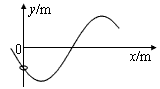
参考答案: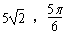
本题解析:
本题难度:一般
4、简答题 如图所示,摆长为L的单摆,当摆球由A经平衡位置O向右运动的瞬间,另一小球B以速度v同时通过平衡位置向右运动,B与水平面无摩擦,与竖直墙壁碰撞无能量损失,问OC间距离x满足什么条件,才能使B返回时与A球相遇?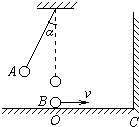
参考答案:A、B相遇一定在O点,B返回O点所用时间为t=2xv,A到达O点时间为t=nT2,
(n=1、2、3…)
所以2xv=nT2,T=2π
本题解析:
本题难度:一般
5、选择题 如图所示,弹簧振子在振动过程中,经过a、b两点的速度相同,历时0.2s。从b点再回到a的最短时间为0.4s,则该振子的振动频率为( )
A.1Hz
B.1.25Hz
C.2Hz
D.2.5Hz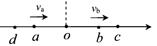
参考答案:B
本题解析:a b关于O点对称,振子一个周期的时间为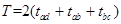 ,由题意可得
,由题意可得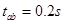 ,因为
,因为 ,所以
,所以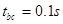 ,由对称可得
,由对称可得 ,所以
,所以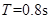 ,根据公式
,根据公式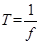 ,所以振子的振动频率为1.25HZ,选B。
,所以振子的振动频率为1.25HZ,选B。
本题难度:一般