时间:2017-03-14 22:01:07
选择题 
如图a所示，用一水平力F拉着一个静止在倾角为θ的光滑斜面上的物体，逐渐增大F，物体做变加速运动，其加速度a随外力F变化的图象如图乙所示，根据图b中所提供的信息可以计算出
A.物体的质量
B.斜面的倾角
C.物体能静止在斜面上所施加的最小外力
D.加速度为6?m/s2时物体的速度
本题答案：ABC
本题解析：分析：对物体进行受力分析，根据牛顿第二定律求出物体加速度与拉力F的关系式，根据图线的斜率和截距可以求出物体的质量和倾角．根据共点力平衡求出物体静止在斜面上施加的最小外力．注意物体做变加速直线运动，速度无法求出．
解答：物体受重力、拉力和支持力，根据牛顿第二定律a=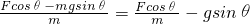
．图线的纵轴截距为-6m/s2，则gsinθ=6，解得斜面的倾角θ=37°．
图线的斜率k=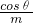
=
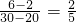，因为sinθ=0.6，则cosθ=0.8，所以m=2kg．
当物体静止时，有Fcosθ=mgsinθ，则施加的最小外力F=mgtanθ=15N，
物体做加速度变化的运动，速度无法求出．故ABC正确，D错误．
故选ABC．
点评：解决本题的关键能够正确地进行受力分析，运用牛顿第二定律求解，以及能够从图线的斜率和截距获取信息．
本题所属考点：【牛顿运动定律】
本题难易程度：【困难】