时间:2017-03-10 11:02:38
选择题 如图所示,细线的一端系一质量为m的小球,另一端固定在倾角为θ的光滑斜面体顶端,细线与斜面平行.在斜面体以加速度a水平向右做匀加速直线运动的过程中,小球始终静止在斜面上,重力加速度为g,小球受到细线的拉力为T,斜面的支持力为FN,则
A.T=m(g sinθ+a cosθ)
B.T=m(g cosθ+a sinθ)
C.FN=m(g cosθ-a sinθ)
D.FN=m(g cosθ+a sinθ)
本题答案:AC
本题解析:试题分析:当加速度a较小时,小球与斜面一起运动,此时小球受重力、绳子拉力和斜面的支持力,绳子平行于斜面;小球的受力如图: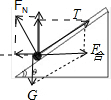
由牛顿第二定律得:Tcosθ-FNsinθ=ma?①?
F合=mgcotθ=ma0
由平衡得:Tsinθ+FNcosθ=mg?②
①②联立得:FN=m(gcosθ-asinθ)
T=m(gsinθ+acosθ)?故AC正确,BD错误.故选AC.
考点:牛顿第二定律;力的合成与分解的运用.
本题所属考点:【牛顿运动定律】
本题难易程度:【一般】