时间:2017-03-05 17:24:32
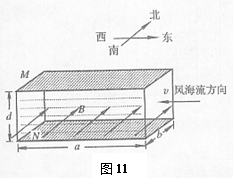
1、计算题 (9分)由于受地球信风带和盛行西风带的影响,海洋中一部分海水做定向流动,称为风海流,风海流中蕴藏着巨大的动力资源。因为海水中含有大量的带电离子,这些离子随风海流做定向运动,如果有足够强的磁场能使海流中的正、负离子发生偏转,便可用来发电。图11为一利用风海流经典的磁流体发电机原理示意图,用绝缘材料制成一个横截面为矩形的管道,在管道的上、下两个内表面装有两块金属板M、N,金属板长为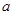 ,宽为
,宽为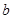 ,两板间的距离为
,两板间的距离为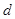 ,将管道沿风海流方向固定在风海流中,在金属板之间加一水平匀强磁场,磁感应强度大小为
,将管道沿风海流方向固定在风海流中,在金属板之间加一水平匀强磁场,磁感应强度大小为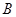 ,方向由南向北,用导线将M、N外侧连接电阻为
,方向由南向北,用导线将M、N外侧连接电阻为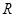 的航标灯(图中未画出)。工作时,海水从东向西流过管道,在两金属板之间形成电势差,可以对航标灯供电,设管道内海水的流速处处相同,且速率恒为
的航标灯(图中未画出)。工作时,海水从东向西流过管道,在两金属板之间形成电势差,可以对航标灯供电,设管道内海水的流速处处相同,且速率恒为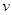 ,海水的电阻率为
,海水的电阻率为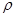 ,海水所受摩擦力与流速成正比,比例系数为
,海水所受摩擦力与流速成正比,比例系数为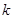 。
。
(1)求磁流体发电机电动势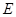 的大小,并判断M、N两板哪个板电势较高;
的大小,并判断M、N两板哪个板电势较高;
(2)由于管道内海水中有电流通过,磁场对管道内海水有力的作用,求此力的大小和方向;
(3)求在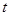 时间内磁流体发电机消耗的总机械能。
时间内磁流体发电机消耗的总机械能。
 |
参考答案:(1)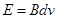 ,N板的电势高
,N板的电势高
(2)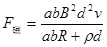 ,方向与
,方向与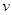 方向相反(水平向东)
方向相反(水平向东)
(3)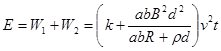
本题解析:(9分)(1)磁流体发电机电动势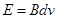 …………(1分)
…………(1分)
用左手定则判断出正离子向N板偏转,因此N板的电势高…………(1分)
(2)两板间海水的电阻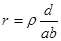 ,回路中的电流
,回路中的电流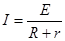 …………(1分)
…………(1分)
磁场对管道内海水的作用力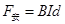
解得: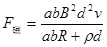 …………(1分)
…………(1分)
方向与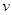 方向相反(水平向东)…………(1分)
方向相反(水平向东)…………(1分)
(3)在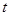 时间内管道中海水移动的距离为
时间内管道中海水移动的距离为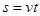 …………(1分)
…………(1分)
在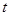 时间内克服摩擦阻力的功
时间内克服摩擦阻力的功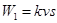 ,克服磁场力做功
,克服磁场力做功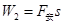 …………(1分)
…………(1分)
在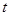 时间内磁流体发电机消耗的总机械能:
时间内磁流体发电机消耗的总机械能: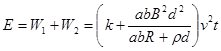 )…………(2分)
)…………(2分)
本题难度:简单
2、计算题 如图所示,边长为L的正方形金属框,质量为m,电阻为R,用细线把它悬挂于一个有界的匀强磁场边缘,金属框的上半部处于磁场内,下半部处于磁场外.磁场随时间变化规律为B=kt(k>0),已知细线所能承受的最大拉力为2mg,求: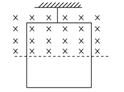
(1)回路中的感应电流大小及方向
(2)从t=0开始,经多长时间细线会被拉断
参考答案:(1)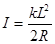 逆时针方向(2)
逆时针方向(2)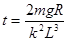
本题解析:解:(1)依电磁感应规律有: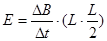 ?…………(1)?(2分)
?…………(1)?(2分)
依 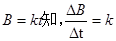 …………(2)?(1分)
…………(2)?(1分)
又 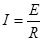 ?……………………(3)?(1分)
?……………………(3)?(1分)
解以上三式得: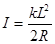 ?(1分)
?(1分)
依据楞次定律知,电流方向为逆时针方向。?(1分)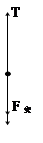
(2)设经时间t,细线刚要被拉断瞬间有: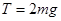 ?…………………………(4)? (1分)
?…………………………(4)? (1分)
则对线框受力分析有: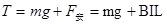 …………(5)? (3分)
…………(5)? (3分)
又t时刻有,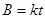 ?………………(6)?(1分)
?………………(6)?(1分)
解(4)、(5)、(6)得:?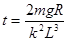 ?(1分)
?(1分)
本题考查的是电磁感应定律和力学综合的问题,根据电磁感应定律求出感应电流,再利用受力分析求得时间;
本题难度:一般
3、计算题 (21分)
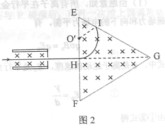
图中左边有一对平行金属板,两板相距为d,电压为V;两板之间有匀强磁场,磁感应强度大小为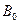 ,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。
,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。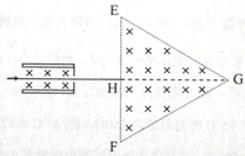
(1)已知这些离子中的离子甲到达磁场边界EG后,从边界EF穿出磁场,求离子甲的质量。
(2)已知这些离子中的离子乙从EG边上的I点(图中未画出)穿出磁场,且GI长为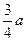 。求离子乙的质量。
。求离子乙的质量。
(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上什么区域内可能有离子到达。
参考答案:
(1)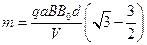 ?
?
(2)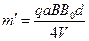 ?
?
(3)所以,磁场边界上可能有离子到达的区域是: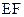 边上从
边上从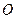 到
到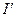 点。
点。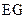 边上从
边上从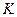 到
到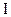 。
。
本题解析:(21分)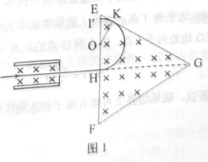
(1)由题意知,所有离子在平行金属板之间做匀速直线运动,它所受到的向上的磁场力和向下的电场力平衡,有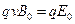 ?①?
?①?
式中,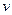 是离子运动的速度,
是离子运动的速度,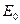 是平行金属板之间的匀强电场的强度,有
是平行金属板之间的匀强电场的强度,有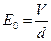 ?②?
?②?
由①②式得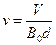 ?③?
?③?
在正三角形磁场区域,离子甲做匀速圆周运动。设离子甲质量为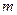 ,由洛仑兹力公式和牛顿第二定律有
,由洛仑兹力公式和牛顿第二定律有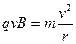 ?④
?④
式中,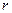 是离子甲做圆周运动的半径。离子甲在磁场中的运动轨迹为半圆,圆心为
是离子甲做圆周运动的半径。离子甲在磁场中的运动轨迹为半圆,圆心为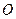 :这半圆刚好与
:这半圆刚好与 边相切于
边相切于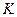 ,与
,与 边交于
边交于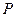 点。在
点。在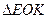 中,
中,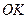 垂直于
垂直于 。由几何关系得
。由几何关系得
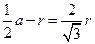 ?⑤
?⑤
由⑤式得
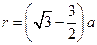 ?⑥
?⑥
联立③④⑥式得,离子甲的质量为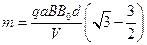 ?⑦?
?⑦?
(2)同理,由洛仑兹力公式和牛顿第二定律有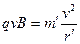 ?⑧
?⑧
式中,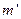 和
和 分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心
分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心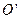 必在
必在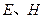 两点之间,又几何关系有
两点之间,又几何关系有 ?⑨
?⑨
由⑨式得
?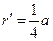 ?⑩
?⑩
联立③⑧⑩式得,离子乙的质量为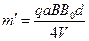 ?(11)
?(11)
(1)?对于最轻的离子,其质量为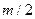 ,由④式知,它在磁场中做半径为
,由④式知,它在磁场中做半径为 的匀速圆周运动。因而与
的匀速圆周运动。因而与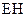 的交点为
的交点为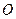 ,有
,有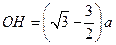 ?(12)
?(12)
(2)当这些离子中的离子质量逐渐增大到m时,离子到达磁场边界上的点的位置从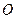 点沿
点沿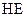 边变到
边变到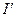 点;当离子质量继续增大时,离子到达磁场边界上的点的位置从
点;当离子质量继续增大时,离子到达磁场边界上的点的位置从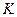 点沿
点沿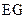 边趋向于
边趋向于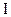 点。
点。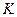 点到
点到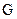 点的距离为
点的距离为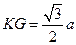 ?(13)
?(13)
(3)所以,磁场边界上可能有离子到达的区域是: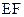 边上从
边上从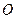 到
到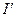 点。
点。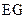 边上从
边上从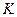 到
到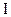 。
。
本题难度:一般
4、选择题 现有一束由a粒子、质子、电子组成的粒子束各自以一定的初速度垂直进入一正交的匀强磁场和匀强电场正方体区域,则下列判断正确的是(?)
A.沿直线通过的粒子的速度由各自的比荷确定
B.沿直线通过的粒子的速度由各自的初动能决定
C.沿直线通过的粒子的速度都相同
D.不沿直线通过的粒子的动能一定不发生变化
参考答案:C
本题解析:沿直线通过的粒子受力平衡,即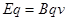 即
即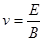 ,所以沿直线通过的粒子的速度都相等,所以该模型又叫速度选择器,不沿直线通过的粒子在沿电场方向直线上必发生位移,所以电场力必做功,即粒子的动能一定发生变化,所以B正确。
,所以沿直线通过的粒子的速度都相等,所以该模型又叫速度选择器,不沿直线通过的粒子在沿电场方向直线上必发生位移,所以电场力必做功,即粒子的动能一定发生变化,所以B正确。
本题难度:一般
5、计算题 (15分)如图所示,正三角形ABC内有B=0.1T的匀强磁场,方向垂直纸面向外,在BC边右侧有平行于BC足够长的挡板EF,已知B点到挡板的水平距离BD=0.5m。某一质量m=4×10-10kg,电荷量q=1×10-4C的粒子,以速度:v0=1×104m/s自A点沿磁场中的AB边射入,恰可从BC边水平射出打到挡板上。不计粒子重力。
(1)求粒子从BC边射出时,射出点距C点的距离和粒子在磁场中运动的时间。
(2)如果在BC至EF区域加上竖直向下的匀强电场,使粒子仍能打到挡板上,求所加电场电场强度的最大值。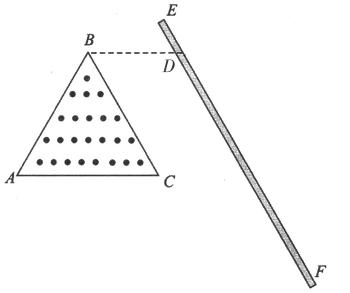
参考答案:(1)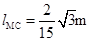 ;
;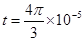 s;(2)
s;(2)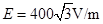 。
。
本题解析:(1)粒子在磁场中的运动轨迹如图: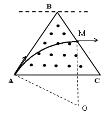
粒子进入磁场后做匀速圆周运动,半径为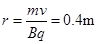 ?(2分)
?(2分)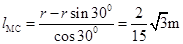 (2分),
(2分),
磁场中的运动时间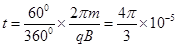 s?(2分)
s?(2分)
(2)当粒子恰好打到板上Q点时,轨迹与板相切,速度方向沿板EF,如图,由类平抛运动的规律,Q点处粒子的速度的反向延长线交水平位移的中点,有lMN=lNP,(2分)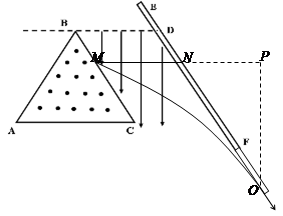
当粒子打到Q点时, 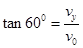 (2分)
(2分)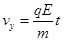 (1分)
(1分)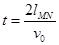 (1分)
(1分)
联立得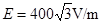 (3分)
(3分)
本题难度:一般