时间:2017-03-05 17:10:17
1、选择题 如图所示，两个折成直角的金属薄板围成足够大的正方形abcd，加上电压，忽略边缘及转角处对电场分布的影响，正方形内部处处可视为方向由a指向c的匀强电场（图中未画出），同时在内部加方向垂直纸面向里的匀强磁场．现在有一个带负电、重力不计的粒子以v0（v0≠0）分别从图示三个方向开始运动，则（ ）
A．只要v0大小合适，可以沿1（ac方向）轨迹直线运动
B．无论v0多大，都不能沿2（平行dc方向）轨迹直线运动
C．只要v0大小合适，可以沿3（db方向）轨迹直线运动
D．只能沿3轨迹加速直线运动
参考答案：A、不论v0大小如何，粒子受到电场力与洛伦兹力不共线，则不可能平衡，因此不可能沿着1（ac方向）轨迹直线运动，故A错误；
B、无论v0多大，粒子受到电场力与洛伦兹力不可能平衡，因此不可能沿着2（平行dc方向）轨迹直线运动，故B正确；
C、只要v0大小合适，则有电场力与洛伦兹力相平衡，可以沿3（db方向）轨迹直线运动，且做匀速直线运动，故C正确，D错误；
故选：BC．
本题解析：
本题难度：简单
2、填空题 如图所示，匀强电场E竖直向下，匀强磁场B垂直纸面向里．现有三个带有等量同种电荷的油滴a、b、c，若将它们分别置入该区域中，油滴a做匀速圆周运动，油滴b向左水平匀速运动，油滴c向右水平匀速运动，则比较三个油滴所受重力Ga、Gb、Gc的大小，最大的是______，最小的是______．
参考答案：
油滴a做匀速圆周运动，可判断其受到的电场力和重力大小相等，方向相反，电场力方向竖直向上，所以带负电；力的关系为：Ga=qE
油滴b向左水平匀速运动，对其受力分析，受竖直向下的重力、竖直向上的电场力和竖直向上的洛伦兹力（由左手定则来判断），三力平衡，即Gb=qE+qvB
油滴c向右水平匀速运动，对其受力分析，受竖直向下的重力、竖直向上的电场力和竖直向下的洛伦兹力（由左手定则来判断），三力平衡，即Gc=qE-qvB
由以上分析可得三个油滴的重力关系为：Gb＞Ga＞Gc
故答案为：Gb，Gc
本题解析：
本题难度：简单
3、计算题 (16分)如图所示，在xoy平面内，y轴左侧有沿x轴正方向的匀强电场，电场强度大小为E；在0＜x＜L区域内，x轴上、下方有相反方向的匀强电场，电场强度大小均为2E；在x＞L的区域内有垂直于xoy平面的匀强磁场，磁感应强度大小不变、方向做周期性变化。一电荷量为q、质量为m的带正电粒子(粒子重力不计)，由坐标为(－L，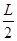
)的A点静止释放。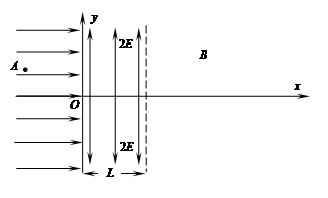
⑴求粒子第一次通过y轴时速度大小；
⑵求粒子第一次射入磁场时的位置坐标及速度；
⑶现控制磁场方向的变化周期和释放粒子的时刻，实现粒子能沿一定轨道做往复运动，求磁场的磁感应强度B大小取值范围。
参考答案：⑴v0＝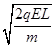
；⑵(L，L)，v＝
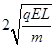，方向与x轴正方向成45°角斜向上；⑶0＜B＜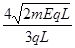
本题解析：⑴粒子在y轴左侧的匀强电场中被加速做直线运动，根据动能定理有：qEL＝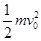
－0
解得粒子第一次通过y轴时速度大小为：v0＝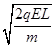
⑵粒子进入偏转电场后作类平抛运动，设其运动时间为t，在x方向上有：L＝v0t
在y方向上有：Δ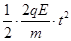y＝
，vy＝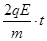
解得：Δy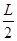＝，vy＝v0
所以粒子第一次射入磁场时的位置坐标为(L，L)
速度大小为：v＝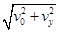
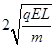＝，方向与x轴正方向成45°角斜向上
⑶在磁场中，粒子做匀速圆周运动，根据向心力公式和牛顿第二定律有：qvB＝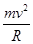
解得粒子做匀速圆周运动的轨道半径为：R＝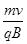
由对称性可知，射出磁场后必须在x轴下方的电场中运动，才能实现粒子沿一定轨道做往复运动，如图所示。
当CC1＝＋＋＝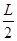
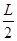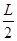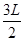时，轨道半径R最小，对应的磁感应强度B最大，粒子紧贴x轴进入y轴左侧的电场
根据图中几何关系有：R2＋R2＝CC12
解得最小半径为：R＝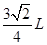
，对应的磁感应强度的最大值为：Bmax＝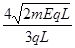
所以磁感应强度大小取值范围：0＜B＜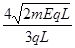
本题难度：一般
4、计算题 如图甲所示，一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L＝1.0m，NQ两端连接阻值R＝3.0Ω的电阻，磁感应强度为B的匀强磁场垂直于导轨所在平面向上，导轨平面与水平面间的夹角θ＝300。一质量m=0.20kg，阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连。细线与金属导轨平行。金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示，已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的1/3，g=10m/s2，求：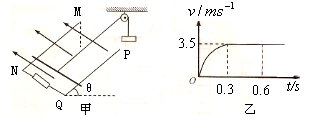
（1）金属棒的最大加速度
（2）磁感应强度的大小
（3）0~0.3s内棒通过的位移;
(4) 金属棒在0~0.6s内产生的热量。
参考答案：（1）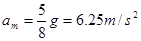
（2）
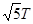（3）0.35m（4）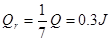
本题解析：（1）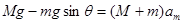
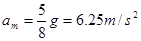
（2）
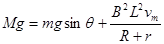
则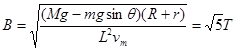
(3)0.3~0.6s内通过的电量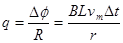
0~0.3s内通过的电量是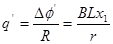
，又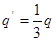
则x1=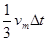
=0.35m
（4）金属棒在0~0.6s内的总位移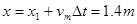
?
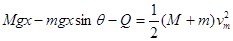
得到Q＝2.1J
金属棒在0~0.6s内产生的热量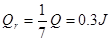
本题考查电磁感应与牛顿第二定律的结合问题，在一开始分析受力求出加速度，根据电量公式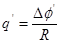
，分析两个过程电荷量关系，求出位移关系，由动能定理求出回路产生的焦耳热，由能量分配确定金属棒的焦耳热
本题难度：一般
5、填空题 如图所示，水平放置的平行金属板A带正电，B带负电，A、B间距离为d，匀强电场的场强为E，匀强磁场的磁感应强度为B，方向垂直纸面向里，今有一带电粒子A、B间竖直平面内做半径为R的匀速圆运动，则带电粒子的转动方向为______时针方向，速率为______．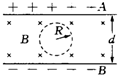
参考答案：由题意可知，粒子之所以能做匀速圆周运动，是因电场力与重力平衡，所以电场力竖直向上，根据电场线的方向，则粒子带负电，再根据左手定则可知，粒子沿着顺时针方向转动．
由洛伦兹力表达式有：
Bqv=mv2R ①
而在竖直方向上合力为零，则有：
qE=mg ②
联立①②解得：
v=gBRE．
故答案为：顺，gBRE．
本题解析：
本题难度：一般