时间:2017-03-05 17:00:42
1、简答题 20世纪40年代,我国物理学家朱洪元先生提出,电子在匀强磁场中作匀速圆周运动时会发出“同步辐射光”,辐射光的频率是电子作匀速圆周运动频率的k倍,大量实验证明,朱洪元先生的上述理论是正确的,并准确测定了k的数值,近年来同步辐射光已被应用于大规模集成电路的光刻工艺中.若电子在某匀强磁场中做匀速圆周运动时产生的同步辐射光的频率为f,电子质量为m,电量为e,不计电子发出同步辐射光时损失的能量及对其速率和轨道的影响
(1)写出电子作匀速圆周运动的周期T与同步辐射光的频率f之间的关系式
(2)求此匀强磁场的磁感应强度B的大小
(3)若电子作匀速圆周运动的半径为R,求子电运动的速率.
参考答案:(1)根据辐射光的频率是电子作匀速圆周运动频率的k倍,及f=1T
得:1T=fk
解得:T=kf?
(2)(3)电子在匀强磁场B中作匀速圆周运动,由电子所受的洛仑兹力f=evB提供向心力.
据牛顿第二定律和圆周运动公式得:
F=Bev=mv2R?
而v=2πRT=2πRfk
解得:B=2πmfke?
答:(1)电子作匀速圆周运动的周期T与同步辐射光的频率f之间的关系式为T=kf;
(2)求此匀强磁场的磁感应强度B的大小为2πmfke;
(3)若电子作匀速圆周运动的半径为R,电子运动的速率为2πRfk.
本题解析:
本题难度:一般
2、选择题 圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B.一带电粒子(不计重力)以某一初速度沿直径方向射入,穿过磁场的时间为t,速度方向偏转60°.如图所示,根据上述条件可求下列哪个物理量( )
A.带电粒子在磁场中运动的半径
B.带电粒子的初速度
C.带电粒子的荷质比
D.带电粒子的质量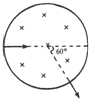
参考答案:A、带电粒子沿半径方向入射,经过磁场偏转60°后又沿半径方向出射,从而画出圆弧对应的弦,确定圆弧的圆心,算出圆心角.再根据运动的时间及周期公式可算出带电粒子的荷质比.但由于不知圆形磁场的半径,则无法求出轨道圆弧的半径,故A错误;
B、带电粒子沿半径方向入射,经过磁场偏转60°后又沿半径方向出射,从而画出圆弧对应的弦,确定圆弧的圆心,算出圆心角.再根据运动的时间及周期公式可算出带电粒子的荷质比.但由于不知圆形磁场的半径,则无法求出轨道圆弧的半径,所以也不能算出粒子的初速度,故B错误;
C、带电粒子沿半径方向入射,经过磁场偏转60°后又沿半径方向出射,从而画出圆弧对应的弦,确定圆弧的圆心,算出圆心角.再根据运动的时间及周期公式可算出带电粒子的荷质比.故C正确;
D、带电粒子沿半径方向入射,经过磁场偏转60°后又沿半径方向出射,从而画出圆弧对应的弦,确定圆弧的圆心,算出圆心角.再根据运动的时间及周期公式可算出带电粒子的荷质比.由于不知带电粒子的电量,所以粒子的质量也无法知道.故D错误;
故选:C
本题解析:
本题难度:一般
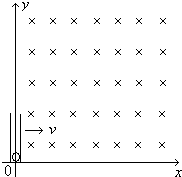
3、简答题 在水平面上有一沿y轴放置的长为L=1m的细玻璃管,在管底有光滑绝缘的带正电的小球.在第一象限中存在磁感应强度为B=1T的匀强磁场,方向如图所示.已知管沿x轴以v=1m/s的速度平动,带电小球的荷质比为
| q m |
| 1 2 |
参考答案: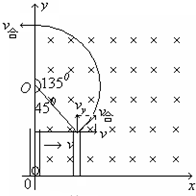
小球在离开管之前随管向右以v平动,同时沿管壁做初速度为零的匀加速运动.
(1)设小球的质量为m,加速度为a,受到的洛伦兹力为f=qvB
由牛顿第二定律有?a=fm=qvBm①
而qm=12②
小球飞出管口所有时间为t,则L=12at2③
联立①②③并代入数据解得:t=2s?④
(2)小球飞出管口时沿管壁方向的速度为vy=at⑤
飞出时的合速度为v合=
本题解析:
本题难度:一般
4、选择题 在水平路面上转弯的汽车,向心力来源于( )
A.重力与支持力的合力
B.滑动摩擦力
C.重力与摩擦力的合力
D.静摩擦力
参考答案:在水平路面上拐弯,向心力来源于静摩擦力,静摩擦力方向指向圆心.故D正确,A、B、C错误.
故选D.
本题解析:
本题难度:简单
5、选择题 如图所示,质量不计的轻杆一端固定于水平轴O上,另一端固定一个质量为m的小球,使杆带动小球在竖直面内绕O轴运动,当小球经过最高点时,以下说法中正确的是

[? ]
 (L为杆长)
(L为杆长)参考答案:ABC
本题解析:
本题难度:一般