高中物理知识点大全《电磁感应中切割类问题》高频考点强化练习（2017年最新版） - 高考物理题库

1、计算题（12分）如图所示，图a表示，空间有一宽为2L的匀强磁场区域，磁感应强度为B，方向垂直纸面向外。abcd是由均匀电阻丝做成的边长为L的正方形线框，总电阻为R。线框以垂直磁场边界的速度v匀速通过磁场区域。在运动过程中，线框ab、cd两边始终与磁场边界平行。线框刚进入磁场的位置x=0，x轴沿水平方向向右。求：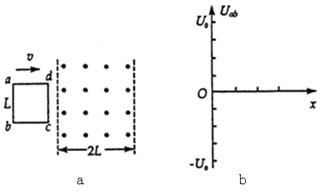

（1）cd边刚进入磁场时，ab两端的电势差，并指明哪端电势高；
（2）线框穿过磁场的过程中，线框中产生的焦耳热；
（3）在b图中，画出ab两端电势差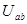随距离变化的图像。其中。

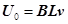参考答案：（1）cd边刚进入磁场时，ab两端的电势差为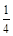BLv，b端电势高；（2）线框穿过磁场的过程中，线框中产生的焦耳热为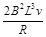；（3）如图所示。

本题解析：（1）dc切割磁感线产生的感应电动势 E=BLv，回路中的感应电流I=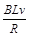，ab两端的电势差U=I?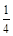R=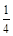BLv，b端电势高。
（2）设线框从dc边刚进磁场到ab边刚进磁场所用时间为t
由焦耳定律得 Q=2I2Rt ，因L=vt，求出Q=。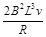
（3）刚进入磁场时，由于b端的电势高，则Uab=-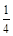BLv。全部进入磁场后，Uab=

本题难度：一般

2、简答题某种超导磁悬浮列车是利用超导体的抗磁作用使列车车体向上浮起，同时通过周期性地变换磁极方向而获得推进动力．其推进原理可以简化为如图所示的模型：在水平面上相距b的两根平行直导轨间，有竖直方向等距离分布的方向相反的匀强磁场B1和B2，且B1=B2=B，每个磁场分布区间的长都是a，相间排列，所有这些磁场都以速度v向右匀速平动．这时跨在两导轨间的长为a宽为b的金属框MNQP（悬浮在导轨正上方）在磁场力作用下也将会向右运动．设金属框的总电阻为R，运动中所受到的阻力恒为f，求：
（1）列车在运动过程中金属框产生的最大电流；
（2）列车能达到的最大速度；
（3）简述要使列车停下可采取哪些可行措施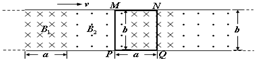？ 91考试网

参考答案：（1）列车起动时金属框产生的电流最大，设为Im
则 Im=2BbvR
（2）分析列车受力可得列车运动的加速度：a=F-fm．
当列车速度增大时，安培力F变小，加速度变小，当a=0时，列车速度达到最大，有：F=f
即? F=2Bb2Bb(v-vm)R
解得：vm=v-Rf4B2b2
（3）要使列车停下可采取措施，如：切断激磁电流，改变磁场运行方向，增大阻力等．
答：
（1）列车在运动过程中金属框产生的最大电流是2BbvR；
（2）列车能达到的最大速度为v-Rf4B2b2；
（3）要使列车停下可采取切断激磁电流，改变磁场运行方向，增大阻力等．

本题解析：

本题难度：一般

3、选择题如图所示装置中，当cd杆运动时，ab杆中的电流方向由a向b，则cd杆的运动可能是（　　）
A．向右加速运动
B．向右减速运动
C．向左匀速运动
D．向左减速运动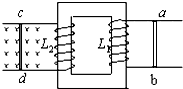

参考答案：A、cd杆向右加速运动时，由右手定则可知，cd棒中产生由d→c的感应电流，感应电动势增大，感应电流也增大，此电流通过线圈L2，线圈产生的磁场增强，穿过线圈L1的磁通量增加，会产生感应电流，由安培定则可知，线圈L2产生的磁场方向向下，穿过L1产生的磁场方向向上，由楞次定律判断可知，ab棒产生的感应电流方向为b→a，不符合题意，故A错误．
B、cd杆向右减速运动时，由右手定则可知，cd棒中产生由d→c的感应电流，感应电动势减小，感应电流也减小，此电流通过线圈L2，线圈产生的磁场减弱，穿过线圈L1的磁通量减小，会产生感应电流，由安培定则可知，线圈L2产生的磁场方向向下，穿过L1产生的磁场方向向上，由楞次定律判断可知，ab棒产生的感应电流方向为a→b，符合题意，故B正确．
C、cd杆向左匀速运动时，由右手定则可知，cd棒中产生由c→d的感应电流，感应电动势不变，感应电流也不变，此电流通过线圈L2，线圈产生的磁场恒定不变，穿过线圈L1的磁通量不变，不产生感应电流，不符合题意，故C错误．
D、cd杆向左减加速运动时，由右手定则可知，cd棒中产生由c→d的感应电流方向，感应电动势减小，感应电流也减小，此电流通过线圈L2，线圈产生的磁场减弱，穿过线圈L1的磁通量减小，会产生感应电流，由安培定则可知，线圈L2产生的磁场方向向上，穿过L1产生的磁场方向向下，由楞次定律判断可知，ab棒产生的感应电流方向为b→a，不符合题意，故D错误．
故选：B

本题解析：

本题难度：简单

4、简答题足够长光滑导轨，竖直放置在垂直于纸面向里的匀强磁场中，已知导轨宽L=0.5m，磁感应强度B=2T．有阻值为0.5Ω，质量为0.2kg的导体棒AB紧挨导轨，沿着导轨由静止开始下落，如图所示，设串联在导轨中的电阻R阻值为2Ω，其他部分的电阻及接触电阻均不计．
问：（1）导体棒AB在下落过程中达到的最大速度为多少？
（2）当导体棒AB的速度为3m/s时，求此时棒的加速度？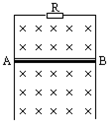

参考答案：（1）导体棒匀速运动时速度最大，
导体棒受到的安培力：F=BIL=B2L2vmR，
由平衡条件得：B2L2vmR=mg，
解得：vm=5m/s；
（2）由牛顿第二定律得：B2L2vR-mg=ma，
解得：a=4m/s2；
答：（1）导体棒AB在下落过程中达到的最大速度为5m/s；
（2）当导体棒AB的速度为3m/s时，此时棒的加速度为4m/s2．

本题解析：

本题难度：一般

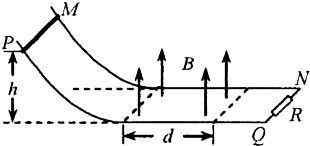
5、选择题如图，MN和PQ是电阻不计的平行金属导轨，其间距为L，导轨弯曲部分光滑，平直部分粗糙，右端接一个阻值为R的定值电阻．平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场．质量为m、电阻也为R的金属棒从高为h处静止释放，到达磁场右边界处恰好停止．已知金属棒与平直部分导轨间的动摩擦因数为u，金属棒与导轨间接触良好．则金属棒穿过磁场区域的过程中（　　）
A．流过金属棒的最大电流为

Bd

2gh

2R

B．通过金属棒的电荷量为

BdL
R

C．克服安培力所做的功为mgh
D．金属棒产生的焦耳热为

1
2

mg（h-μd）