时间:2017-03-05 16:47:29
1、计算题 如图所示,两带电平行板A、B间的电场为匀强电场,场强E=4.0×102V/m,两板相距d=16cm,板长L=30cm。一带电量q=1.0×10-16C、质量m=1.0×10-22kg的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子所受重力,求: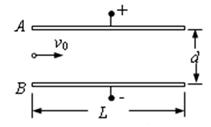
(1)粒子带何种电荷?
(2)要使粒子能飞出电场,粒子飞入电场时的速度v0至少为多大?
(3)粒子正好从B板右端飞出时的速度多大?
参考答案:(1)正电荷(2)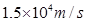 (3)
(3)
本题解析:(1)粒子向负极板偏转,所以粒子带正电
(2)当粒子恰好从B板偏出时,在垂直于板方向上有: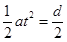 ?
?
在沿板方向上有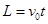
对粒子应用牛顿第二定律得: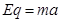
联立以上方程得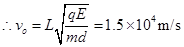
(3)运动到B板右端时,垂直于板方向的速度为: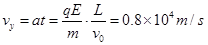
和速度为: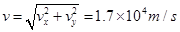
本题难度:一般
2、选择题 一个质量为m、电荷量为+q的小球以初速度v0水平抛出,在小球经过的竖直平面内,存在着若干个如图所示的无电场区和有理想上下边界的匀强电场区,两区域相互间隔、竖直高度相等,电场区水平方向无限长,已知每一电场区的场强大小相等、方向均竖直向上,不计空气阻力,下列说法正确的是 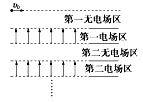
[? ]
A.小球在水平方向一直做匀速直线运动
B.若场强大小等于mg/q,则小球经过每一电场区的时间均相同
C.若场强大小等于2mg/q,则小球经过每一无电场区的时间均相同
D.无论场强大小如何,小球通过所有无电场区的时间均相同
参考答案:AC
本题解析:
本题难度:一般
3、选择题 如图所示,两平行板竖直放置,A、B两小孔正对,两极板间所加电压为500 V,一个动能为400 eV的电子从A孔沿垂直于板面方向射入电场,经一段时间后离开电场,则电子离开电场时动能为(?)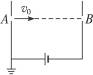
A.900 Ev? B.500 eV? C.400 eV? D.100 eV
参考答案:C
本题解析:由图可知:电子在匀强电场中做匀减速运动,当电子克服电场力做功等于400 eV时,电子的速度便减小到0,之后返回,当到后返A点时,电场力做功为0, 由动能定理知:电子的动能仍然不变,故应选C.本题很容易错选D,那是由于没有考虑电子在电场中减速到0后会原路返回,而直接套公式eU=Ek0-Ek,即500 eV="400" eV-Ek,所以Ek="-100" eV,便得到错误结果D.
本题难度:简单
4、选择题 如图所示,三个等势面上有a、b、c、d四点,若将一正电荷由c经a移到d点,电场力做正功W1;若由c经b移到d点,电场力做正功W2.则W1与W2,c、d两点电势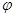 c、
c、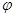 d关系为( )
d关系为( )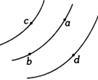
A.W1>W2,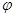 c>
c>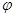 d
d
B.W1<W2,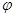 c<
c<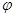 d
d
C.W1=W2,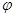 c<
c<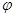 d
d
D.W1=W2,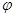 c>
c>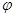 d
d
参考答案:D
本题解析:由电场力做功与路径无关可知,W1=W2,AB错;由Wcd=qUcd得到Wcd>0,q>0,所以Ucd>0,Ucd=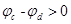 ,所以
,所以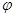 c>
c>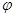 d,D对,C错。
d,D对,C错。
考点:本题考查电场力做功与路径无关,电场力做功公式,电势差与电势间的关系式。
点评:学生清楚电场力做功与重力做功相似,都与路径无关,在用电场力做功的公式和电势差的公式时,注意下角标的顺序要一致。
本题难度:一般
5、计算题 如图所示,一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出。已知两极板长为l,间距为d,求:
(1)如果带电粒子的速度变为2v0,则离开电场时,沿场强方向偏转的距离y为多少?
(2)如果带电粒子的速度变为2v0,板长l不变,当它的竖直位移仍为d时,它的水平位移为多少?(粒子的重力忽略不计) 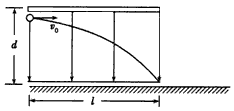
参考答案:解:因为带电粒子在电场中运动,受到的电场力与速度无关,所以加速度是一定的 ,解得
,解得
(1) l=2v0t" 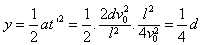
(2)如图所示,将速度反向延长交上板的中点,由相似三角形对应边成比例有
 ,解得x"=1.5l
,解得x"=1.5l
所以水平位移x=l+x"=2.5l
本题解析:
本题难度:困难