时间:2017-03-05 16:21:23
1、选择题 一小球以初速度v0竖直上抛，它能到达的最大高度为H，问下列几种情况中，哪种情况小球可能达到高度H（忽略空气阻力）（ ）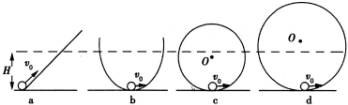
A．图a，以初速v0沿光滑斜面向上运动
B．图b，以初速v0沿光滑的抛物线轨道，从最低点向上运动
C．图c（H＞R＞
| H 2 |
参考答案：小球以v0竖直上抛的最大高度为h，到达最大高度时速度为0，
A、B、小球到达最高点的速度可以为零，根据机械能守恒定律得，mgh+0=mgh′+0．则h′=h．故AB可能．
C、小球到达最高点的速度不能为零，所以小球达不到最高点就离开轨道做斜抛运动．故C不可能．
D、小球运动到最高点时速度可以为零，根据机械能守恒定律可知，小球能达到最高点即高h处，故D可能．
故选ABD．
本题解析：
本题难度：一般
2、计算题 一根长为L的轻杆，一端固定一质量为m的小球A，另一端固定在水平转动轴上.现使小球绕杆的另一端的转轴在竖直平面内做圆周运动，如图.试求：
（1）假设小球转至最低点时，小球的速度大小为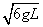
，求此时杆对小球的作用力的大小；
（2）假设小球转至最高点时，小球的速度大小为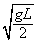
，此时杆对小球的作用力是支持力还是拉力？此力为多大？
参考答案：（1）7mg；
（2）支持力，mg/2
本题解析：
本题难度：一般
3、计算题 如图所示，倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切，切点为B，整个轨道处在竖直平面内。一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑进入圆环轨道。接着小滑块从圆环最高点C水平飞出，恰好击中导轨上与圆心O等高的P点，不计空气阻力。求：
（1）滑块运动到圆环最低点时对圆环轨道压力的大小；
（2）滑块与斜轨之间的动摩擦因数。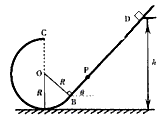 
参考答案：解：（1）小滑块从C点飞出来做平抛运动，水平速度为
。?
，
解得
小滑块在最低点时速度为V由机械能守恒定律得
，
牛二定律：
，
牛三定律得：
（2）DB之间长度
从D到最低点过程中，又动能定理
。
本题解析：
本题难度：困难
4、计算题 如图所示，在圆柱形屋顶中心天花板上O点，挂一根L=3m的细绳，绳的下端挂一个质量m为0.5kg的小球，已知绳能承受的最大拉力为10N，小球在水平面内做圆周运动．当速度逐渐增大到绳断裂后，小球以v=9m/s的速度落在墙角边．求这个圆柱形房屋的高度H和半径R．(g取10m/s2)
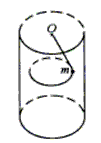
参考答案：H=3.3m；R=0.3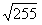
m
本题解析：
本题难度：一般
5、简答题 长L=0.5m、质量可忽略的杆，其下端固定在O点，上端连接着一个零件A，A的质量为m=2kg，它绕O点作圆周运动，如图所示，在A点通过最高点时，求在下列两种情况下杆受的力：
（1）A的速率为1m/s；
（2）A的速率为4m/s．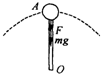
参考答案：小球受到的重力为G=mg=2×10N=20N
（1）A的速率为1m/s，此时需要的向心力为F向1=mv2L=2×120.5N=4N
根据合力提供向心力mg-FN1=F向1
所以FN1=mg-F向1=20N-4N=16N，方向向上
根据牛顿第三定律，杆受到的力竖直向下，大小为16N．
（2）A的速率为4m/s，此时需要的向心力为F向2=mv2L=2×420.5N=64N
根据合力提供向心力mg+FN2=F向2
所以FN2=F向2-mg=64N-20N=44N，方向向下
根据牛顿第三定律，杆受到的力竖直向上，大小为44N．
答：（1）A的速率为1m/s时，杆受到的力竖直向下，大小为16N．
（2）A的速率为4m/s时，杆受到的力竖直向上，大小为44N．
本题解析：
本题难度：一般