时间:2017-03-02 10:35:52
1、简答题 如图所示一对光滑的平行金属导轨间距为L，与水平面夹角为θ，一金属杆ab垂直金属导轨放置，整个装置置于磁感应强度为B的匀强磁场中，磁感应强度垂直水平面方向向上，设金属杆ab的质量m，两条轨间所接电阻为R，其余部分的电阻忽略不计．若导轨足够长，求：
（1）金属杆沿导轨向下运动的最大速度？
（2）当金属杆以最大速度运动时，导轨对金属杆的支持力．
参考答案：金属杆沿导轨向下运动时产生感应电流由b流向a，所以金属杆所受安培力水平向右，
磁场竖直向上，金属杆速度沿斜面向下，所以金属棒切割磁感线的实际速度是Vcosθ，
电动势大小为：E=BLVcosθ，①
当金属杆沿导轨向下运动的最大速度时，金属杆受力平衡，
故沿斜面方向：mgsinθ=F安cosθ，②
F安=BIL? ③
由①②③解得：V=mgRtanθB2L2cosθ
垂直沿斜面方向：mgcosθ+F安sinθ=FN
解得：FN=mg（cosθ+tanθsinθ）
答：（1）金属杆沿导轨向下运动的最大速度mgRtanθB2L2cosθ
（2）当金属杆以最大速度运动时，导轨对金属杆的支持力mg（cosθ+tanθsinθ）
本题解析：
本题难度：一般
2、计算题 （12分）如图所示，B、C两个小球均重G，用细线悬挂而静止于A、D两点。求：
（1）AB和CD两根细线的拉力各多大？
（2）细线BC与竖直方向的夹角是多少？
参考答案：（1）1.732G? G（2）60o
本题解析：(1)整体法：正交分解可得：
FAB=2Gcos30o=1.732G? (3分)
FCD=2Gcos60o=G(3分)
(2)对C球受力分析得：FBCsinθ= Gsin60o?(2分)
Gcos60o+ FBCcosθ=G?(2分)
θ=60o?(2分)（其他做法也可得分）
本题考查受力平衡问题，现已整体为研究对象，分析受力情况，由正交分解得到水平方向和竖直方向的平衡式，求解即可，再以C球为研究对象，分析受力情况，同理求得角度
本题难度：一般
3、选择题 如图所示，在倾角为θ的斜面上放一质量为m的小球，小球被竖直的木板挡住，若斜面和木板都是光滑的，则（?）
A．球对斜面的压力为mgcosθ
B．球对斜面的压力为
C．球对挡板的压力为mg tgθ
D．当挡板从竖直位置放到水平位置过程中，球对斜面的压力一直减小
参考答案：BC
本题解析：分析：以小球为研究对象，将重力按效果进行分解，作出力分解图，由几何知识求出球对斜面和挡板的压力．运用作图法，分析在挡板从竖直位置放到水平位置的过程中球对斜面的压力如何变化．
解答：解：
A、B以小球为研究对象，将重力按效果进行分解，作出力分解图，如图1．球对斜面的压力等于F2=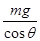
．故A错误，B正确．
C、球对挡板的压力等于F1=mgtanθ．故C正确．
D、如图2所示，在挡板从竖直位置放到水平位置的过程中，F2不断减小，则球对斜面的压力一直减小直到零．故D正确．
故选BCD
点评：本题运用分解法研究物体的平衡问题，也可以采用合成法或正交分解法进行研究．
本题难度：简单
4、选择题 如图所示，两个光滑小球P、Q先后卡在宽度不同、内壁光滑的两个槽中．甲、乙两图中球P对槽底的压力分别为FA、
，对左侧壁B处和
处的压力分别为FB、
，球Q对右侧壁C处和
处的压力分别为FC、
，则?（?）
A．FA=，FB=，FC=
B．FA=，FB=－FC，=－
C．FA
，FB=－FC，=－
D．FA，FB
，FC
参考答案：B
本题解析：由整体法，可得FA=，FB=－FC，=－，即B正确。
本题难度：一般
5、选择题 如图所示，用三根轻细绳AO,BO,CO悬吊着质量为m的物体处于静止状态，AO与竖直方向的夹角为30°，BO沿水平方向，设AO,BO,CO的张力大小分别为F1,F2,F3，则这三个力的大小关系为（?）
A．F1>F2>F3
B．F1>F3>F2
C．F3>F1>F2
D．F1>F2=F3
参考答案：B
本题解析：以节点O为研究对象根据受力平衡，可知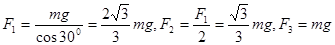
，则三个力的关系为.F1>F3>F2，选B
本题难度：简单