时间:2017-03-01 00:20:58
1、实验题 在用如图甲所示的装置“验证机械能守恒定律”的实验中，打点计时器接在频率为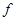
的交流电源上，从实验中打出的几条纸带中选出一条理想纸带，如图乙所示，选取纸带上打出的连续４个点
、
、
、
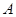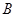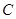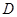，各点距起始点Ｏ的距离分别为
、
、
、
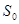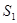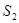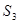，已知重锤的质量为
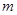，当地的重力加速度为
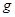，则：
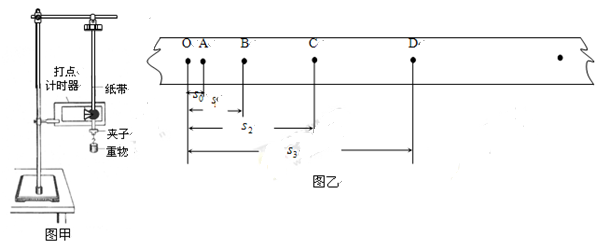
①从打下起始点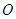
到打下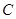点的过程中，重锤重力势能的减少量为
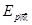＝?，重锤动能的增加量为
＝?。
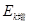②若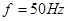
，且测出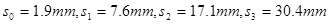
，可求出当地的重力加速度
??
。
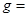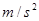参考答案：①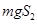
?
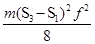?②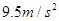
本题解析：①重锤拉动纸带下落，虽然纸带和打点计时器有摩擦，但重锤的质量很大，也就重力很大，摩擦力可以忽略不计，整个过程可以看成机械能守恒，那么重锤下落过程中减少的重力势能为EP减=mgs3，C点的瞬时速度为vc=(s3-s1)/2T，此过程中增加的动能为Ek增=mvc2/2=m(s3-s1)2/8T= m(s3-s1)2f/8。②由mgs3= m(s3-s1)2f/8，代入数据，得g=9.5m/s2。
本题难度：一般
2、实验题 （6分）探究力对原来静止的物体做的功与物体获得的速度的关系，实验装置如图所示，实验主要过程如下：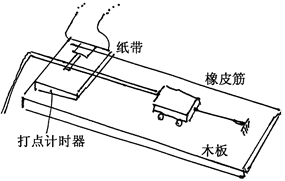
（1）设法让橡皮筋对车做的功分别为W、2W、3W、……
（2）分析打点计时器打出的纸带，求出小车的速度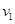
、
、
……
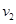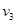（3）作出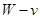
草图
（4）分析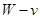图，如果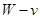图象是一条直线，表明
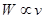；如果不是直线，可考虑是否存在
，
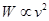等关系。
以下关于该实验的说法中有一项不正确的是（?）
A．本实验设法让橡皮筋对小车做的功分别为W、2W、3W……所采用的方法是选用同样的橡皮筋，并在每次实验中，使橡皮筋拉伸的长度保持一致。当用1条橡皮筋进行实验时，橡皮筋对小车做的功为W，用2条、3条……橡皮筋并在一起进行第2次、第3次……实验时，橡皮筋对小车做的功分别是2W、3W……
B．小车运动中会受到阻力，补偿的方法，可以使木板倾斜。
C．某同学在一次实验中，得到一条记录纸带，纸带上打出的点，两端密，中间疏，出现这种情况的原因，可能是没有使木板倾斜或倾角太小。
D．根据记录纸带上打出的点，求小车获得速度的方法，是以纸带上第一点到最后一点的距离来进行计算。
参考答案：D
本题解析：
试题分析:当橡皮筋伸长量按倍数增加时，功并不简单地按倍数增加，变力功一时无法确切测算．因此我们要设法回避求变力做功的具体数值，可以用一根橡皮筋做功记为W，用两根橡皮筋做功记为2W，用三根橡皮筋做功记为3W…，从而回避了直接求功的困难，故选项A正确。小车阻力补偿的方法是平衡摩擦力，选项B正确。如果没有平衡摩擦力或没有使木板倾斜或倾角太小，则在小车获得的最大速度后，由于过一段距离后又被橡皮筋反拉着，导致速度减小，出现“两端密、中间疏”现象，故选项C正确。本实验的目的是探究橡皮绳做的功与物体获得速度的关系，这个速度是指橡皮绳做功完毕时的速度，而不是整个过程的平均速度，所以D选项是错误的，故选D。本题选不正确的故选D。
本题难度：一般
3、实验题 如图所示，是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带，纸带上两相邻计数点间还有四个点没有画出，，其中x1＝7.05cm、x2＝7.68cm、x3＝8.33cm、x4＝8.95cm、x5＝9.61cm、x6＝10.27cm。
（1）下表列出了打点计时器打下B、D、F时小车的瞬时速度，请在表中填入打点计时器打下C、E两点时小车的瞬时速度（保留三位有效数字）。
| 位置 | B | C | D | E | F |
| 速度（m·s－1） | 0.737 | ? | 0.864 | ? | 0.994 |
参考答案：（1）0.801 m/s ?0.928 m/s?（2）如图所示?（3） 0.61-0.66 m/s2? .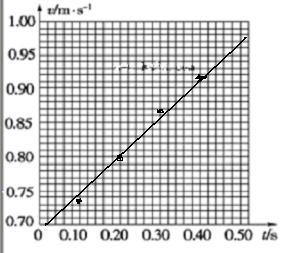
本题解析：根据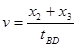
计算C点的速度为0.801 m/s，根据
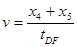?计算E点的速度为0.928 m/s，打点计时器打下A两点时的瞬时速度为
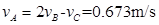，根据速度—时间关系图线可以得到图像的斜率即加速度的大小的范围为0.61-0.66 m/s2。
本题难度：一般
4、填空题 在一次实验时，如果某同学不知道实验所用的交流电源的实际频率已经超过
50Hz,那么他估算出来的平均速度值与真实值相比
（填偏大、偏小或相等）
参考答案：偏小
本题解析：频率大，则周期偏小，平均速度等于位移比上时间，因为时间测量值偏大所以他估算出来的平均速度值与真实值相比偏小。
本题难度：简单
5、简答题 在如图所示的装置中，物体A和C的质量分别为m1、m2，弹簧D、B、E的劲度系数分别为k1、k2、k3，不计弹簧和细绳的质量，不计滑轮的摩擦．当弹簧E处在水平位置且未发生形变时，其右端点位于a位置．将弹簧E的右端点沿水平方向缓慢地从a位置拉到b位置时，弹簧E的拉力大小恰好等于A的重力．求：
（1）当弹簧E处在水平位置且未发生形变时，弹簧D的形变量．
（2）在弹簧E的右端点从a位置拉到b位置的过程中，物体A上升的高度是多少？a、b间的距离是多大？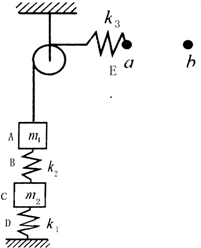
参考答案：（1）当弹簧E未发生形变时弹簧B、D都处于压缩状态，设压缩量分别为xB、xD．对于物体A和C、弹簧B整体，根据平衡条件和胡克定律有
对于物体A和C、弹簧B整体，k1xD=（m1+m2）g
解得弹簧D的形变量为xD=(m1+m2)gk1
对于物体A，k2xB=m1g
（2）当弹簧E的右端点拉到b位置时，因弹簧E的拉力大小恰好等于A的重力，说明此时弹簧E处于伸长状态，且伸长量xE=m1gk3
此时弹簧B恢复原长，弹簧D的压缩量变为xD′=m2gk1
所以物体A上升的高度为h=xD-xD′+xB
解得h=m1g(1k1+1k2)
ab间的距离为ab=h+xE
ab=m1g(1k1+1k2+1k3)
答：（1）弹簧D的形变量xD=(m1+m2)gk1．
（2）物体A上升的高度是h=m1g(1k1+1k2)，a、b间的距离是ab=m1g(1k1+1k2+1k3)．
本题解析：
本题难度：一般