时间:2017-03-01 00:07:42
1、选择题 A、B两个质量不等的小球用长度不等的细线栓在同一点，小球在同一水平面内做匀速圆周运动，如图所示，则它们的（ ）
A．运动周期相等 B．运动线速度相等
C．向心加速度相等 D．受到绳的拉力相等
参考答案：A
本题解析：小球做匀速圆周运动，则合力提供向心力，即小球所受拉力与重力的合力指向圆心，设细绳与竖直方向的夹角为θ，由题意知：Lcosθ是相等的。由三角形定则F向=Gtanθ=ma向=
,F拉=
m、θ不同，则a、v、F拉不同，BCD错误；小球做圆周运动的半径R=Lsinθ,由F向=Gtanθ=
=
得T=
，周期相等，A正确。
考点：本题考查向心力公式的运用。
本题难度：一般
2、填空题 设质量相同的两人甲和乙，甲在赤道上，乙在北纬45°，他们随地球一起转动，则两者线速度大小之比vA：vB=_________，他们受的向心力大小之比FA：FB="_______."
参考答案：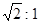
,
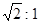
本题解析：由于都在地球上，因此角速度相等，即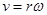
可知线速度之比为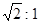；根据向心力公式则
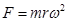，所以向心力之比也为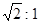
点评：本题考查了匀速圆周运动过程中向心力、线速度的计算
本题难度：一般
3、选择题 火星和地球绕太阳运行的轨道视为圆周。已知火星和地球绕太阳运动的周期之比，由此可求得
A．火星和地球的质量之比
B．火星和地球表面的重力加速度之比
C．火星和地球绕太阳运行速度大小之比
D．火星和地球受到的太阳的万有引力之比
参考答案：C
本题解析：根据开普勒行星运动定律可知，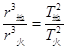
，即已知火星和地球绕太阳运动的周期之比，可求得火星和地球绕太阳运动的半径之比，根据
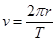可求得火星和地球绕太阳运行速度大小之比，故选项C正确；故选C.
考点：万有引力定律的应用.
本题难度：一般
4、简答题 在水平转台上有一两端固定的水平横杆，杆上套一质量为m的小球（可视作质点）。球可沿杆无摩擦地滑动，现用两根劲度系数均为K的轻弹簧（也套在横杆上）将小球拴住，横杆与轴O在同一竖直平面内，轴O位于水平转台的中央，转台静止时两根弹簧均未有形变，小球所在点P轴O的距离为L，如图所示，转台以角速度ω绕竖直轴O旋转时，小球移到了另一点P′，与横杆保持相对静止，这时P′与P点之间的距离△L＝？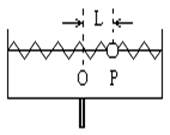
?
参考答案：
本题解析：当小球移到P′点时，右弹簧压缩△L， 左弹簧伸长△L，它们对球的合力
本题难度：简单
5、选择题 用原子级显微镜观察高真空度的空间,结果发现有一对分子甲和乙环绕一个共同“中心”旋转,从而形成一个“双星”体系,观察中同时发现此“中心”离甲分子较近,如果这两个分子间距离为r=r0时,其间相互作用力(即分子力)恰好为零,那么在上述“双星”体系中(? )
A．甲?乙两分子间距离一定小于r0
B．甲?乙两分子间距离一定大于r0
C．甲的速度一定大于乙的速度
D．甲的质量一定大于乙的质量
参考答案：BD
本题解析：因为“双星”分子绕“中心”旋转时的向心力由分子引力提供,所以甲?乙两分子间距离一定大于r0,B对;“双星”体系的两个分子的向心力和角速度大小相等,v=ωr,根据题意r甲<r乙,所以v甲<v乙,C选项错误;由m甲ω2r甲=m乙ω2r乙,得D选项正确.
本题难度：一般