时间:2017-02-28 23:49:13
1、选择题 沿高度相同,坡度不同,粗糙程度也不同的斜面向上拉同一个物体 到顶端,在下列说法中正确的是(?)
A.沿坡度小,长度大的斜面上升克服重力做的功多
B.沿坡度大,粗糙程度大的斜面上升克服重力做的功多
C.沿坡度长,粗糙程度大的斜面上升克服重力做的功多
D.以上几种情况下克服重力所做的功一样多
参考答案:D
本题解析:克服重力做功mgh,只与高度h有关,与波度和其他因素无关,D对;
本题难度:简单
2、选择题 质量为m的物体,在距地面h高处以
| 1 3 |
| 2 3 |
| 2 3 |
| 2 3 |
参考答案:A、根据重力做功与重力势能变化的关系得:
wG=-△Ep
由静止竖直下落到地面,在这个过程中,
wG=mgh,所以重力势能减小了mgH.故A错误.
B、由除了重力和弹簧弹力之外的力做功量度机械能的变化得出:
w外=△E
由静止竖直下落到地面,在这个过程中,根据牛顿第二定律得:
F合=mg-f=ma=13mg
f=23mg
物体除了重力之外就受竖直向上的阻力,
w外=wf=-23mgh
所以物体的机械能减小了23mgh,故B正确.
C、重力对物体做功wG=mgh,故C正确.
D、根据动能定理知道:
w合=△Ek
由静止竖直下落到地面,在这个过程中,
w合=F合h=13mgh,
所以物体的动能增加了13mgh,故D错误.
故选BC.
本题解析:
本题难度:一般
3、简答题 物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动的动能EK与角速度ω的关系.某同学采用了下述实验方法进行探索:先让砂轮由动力带动匀速旋转测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮从脱离动力到停止转动的过程中转动的圈数为n,通过分析实验数据,得出结论.经实验测得的几组ω和n如下表所示:另外已测得砂轮转轴的直径为1cm,转轴间的摩擦力为10/π(N)
| ω/rad-s-1 | 0.5 | 1 | 2 | 3 | 4 n 5.0 20 80 180 320 EK/J |
参考答案:(1)因为摩擦力做功使得动能减小,对砂轮运用动能定理得,EK=f?πD?n
代入解得EK=0.1n
代入n,解得,Ek第一格为0.5,第二格为2.0,第三格为8.0.
(2)由表中ω和EK的相应数据得,发现动能为角速度平方的两倍,则:
EK=2ω2.
故答案为:(1)0.5,2.0,8.0 (2)EK=2ω2
本题解析:
本题难度:一般
4、选择题 一个物体从某一高度自由落下,落在直立于地面上的轻弹簧上,如图所示,在A点物体开始与弹簧接触,到B点时,物体速度为零,然后被弹回,下列说法中正确的是( )
A.物体从A下降到B的过程中,动能不断减小
B.物体从A下降到B的过程中,弹性势能不断减小
C.物体从A下降到B的过程中,动能先增大后减小
D.物体从A下降到B的过程中,动能与重力势能的总和不断变小
参考答案:物体A点接触弹簧开始到将弹簧压缩到最短B点的过程中:
物体刚接触弹簧时,弹簧的弹力小于物体的重力,物体所受合力向下,物体向下加速运动,
当弹簧的弹力和物体的重力相等时,物体所受合力为零,物体继续向下运动,
然后弹力大于了重力,物体受到的合力向上,物体做减速运动,直至速度减小到零.
A、由以上分析可知物体从A到B运动过程中,速度先增大后减小,物体动能先增大后减小,故A错误,C正确
B、物体从A下降到B的过程中,弹簧的形变量越来越大,弹簧的弹性势能越来越大,故B错误;
D、物体从A下降到B的过程中,要不断克服弹簧的弹力做功,物体的机械能逐渐减小,即物体的动能与势能之和不断减小,故D正确;
故选CD.
本题解析:
本题难度:简单
5、选择题 如图所示,质量为m的物体放在水平地面上,物体上方安装一劲度系数为k的轻弹簧,在弹簧处于原长时,用手拉着其上端P点很缓慢地向上移动,直到物体脱离地面向上移动一段距离.在这一过程中,P点的位移为H,则物体重力势能的增加量为( )
A.mgH
B.mgH+m2g2/k
C.mgH-m2g2/k
D.mgH-mg/k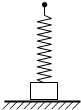
参考答案:弹簧的形变量x=mgk,则物体上升的高度h=H-x=H-mgk
则重力势能的增加量△Ep=mgh=mgH-m2g2k.故C正确,A、B、D错误.
故选C.
本题解析:
本题难度:简单