时间:2017-02-28 23:34:12
1、选择题 某人用手将1Kg物体由静止向上提起1m ,这时物体的速度为2m/s，则下列说法正确的是（g=10m/s）（?）
A．手对物体做功10J
B．合外力做功2J
C．合外力做功12J
D．物体克服重力做功12J
参考答案：B
本题解析：由动能定理
，合外力做功等于动能增量为2J，B对；克服重力做功mgh=10J，D错；
本题难度：简单
2、计算题 如图所示，质量是20kg的小车，在一个与斜面平行的200N的拉力作用下，在斜面底部由静止开始沿斜面前进了3m，斜面的倾角为300，小车与斜面间的摩擦力忽略不计，斜面底部为零势能面．求:此时物体的重力势能为多少?物体的动能为多少?拉力F做的功是多少?
参考答案：Ep=300J? 600J? 300J
本题解析：重力做功为：
,所以重力势能为：Ep=300J?
拉力做的功
=
=600J?
根据动能定理可得：动能Ek=600J－300J=300J
点评：重力做多少功，重力势能就变化多少，与其他力无关，重力势能与零势能点的选取有关，
本题难度：一般
3、简答题 质量为M、长为L的小车，固定在地面上，一个质量为m的小物体（可不计大小）以水平速度v0从小车一端沿表面滑行，小物体从小车另一端滑离小车时，速度减为
| v0 2 |
参考答案：小车固定在地面时，设物体与小车间摩擦力为f，由动能定理
-fL=12m(v02)2-12mv20?（1）
把小车放在光滑水平地面上时，小物体与小车间摩擦力仍为f．设小物体相对小车滑行距离为L时，跟小车相对静止（未能滑离小车）共同速度为V，
由动量守恒定律mv0=（M+m）v?（2）
设这过程小车向前滑行距离为S．由动能定理
对小车运用动能定理有
fS=12Mv2?（3）
对小物体运用动能定理有
-f（L+S）=12Mv2-12mv20?
由（2）（3）（4）解出
fL′=12mv20?（MM+m）?（5）
L′≤L 且fL=38mv20?（6）
比较（5）（6）解出
M≤3m，只要M＞3m小物体就能滑离小车．
答：欲使小物体仍能滑离小车．那么小车的质量M和小物体质量m应满足M＞3m．
本题解析：
本题难度：一般
4、计算题 有一个固定竖直放置的圆形轨道，半径为R，由左右两部分组成。如下图所示，右半部分AEB是光滑的，左半部分BFA是粗糙的。现在最低点A给一质量为m的小球一个水平向右的初速度，使小球沿轨道恰好运动到最高点B，小球在B点又能沿BFA回到A点，到达A点时对轨道的压力为4mg。求：
(1)小球的初速度v0；
(2)由B经F回到A的过程中克服摩擦力所做的功。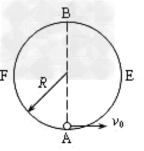
参考答案：解：(1)小球恰好到达B点， 小球由AEB到B点的速度是：
，
?
由动能定理
，
得
?
(2)由于回到A点时对轨道压力为4mg
根据牛顿定律：
，
?
小球由B经F回到A的过程中，
由
和
(或Wf＝E0-EA＝
=mgR0)?
得Wf=mgR
本题解析：
本题难度：一般
5、填空题 物体从高出地面H处由静止自由落下，不考虑空气阻力，落至地面进入沙坑h停止，求物体在沙坑中受到的平均阻力与重力之比为______．
参考答案：对整个过程运用动能定理得：
mg△h-.fh=0-0
解得：.fmg=H+hh
故答案为：H+hh
本题解析：
本题难度：一般