时间:2017-02-28 23:24:51
1、选择题 如右图所示,将一个矩形小线圈放在一个大匀强磁场中,线圈平面平行于磁感线,则线圈中有感应电流产生的是 (? )
A.当矩形线圈做平行于磁感线的平动
B.当矩形线圈做垂直于磁感线的平行移动
C.当矩形线圈绕AB边做转动时
D.当矩形线圈绕BC边做转动时
参考答案:C
本题解析:当闭合回路磁通量发生变化时,回路中有感应电流。C对。
本题难度:简单
2、计算题 如图所示,在水平面上固定一光滑金属导轨HGDEF,EF∥GH,DE=EF=DG=GH=EG=L.一质量为m足够长导体棒AC垂直EF方向放置于在金属导轨上,导轨与导体棒单位长度的电阻均为r.整个装置处在方向竖直向下、磁感应强度为B的匀强磁场中.现对导体棒AC施加一水平向右的外力,使导体棒从D位置开始以速度v0沿EF方向做匀速直线运动,导体棒在滑动过程中始终保持与导轨良好接触.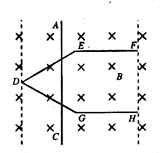
小题1:求导体棒运动到FH位置,即将离开导轨时,FH两端的电势差.
小题2:关于导体棒运动过程中回路产生感应电流,小明和小华两位同学进行了讨论.小明认?为导体棒在整个运动过程中是匀速的,所以回路中电流的值是恒定不变的;小华则认?为前一过程导体棒有效切割长度在增大,所以电流是增大的,后一过程导体棒有效切?割长度不变,电流才是恒定不变的.你认为这两位同学的观点正确吗?请通过推算证?明你的观点.
小题3:求导体棒从D位置运动到EG位置的过程中,导体棒上产生的焦耳热.
参考答案:
小题1: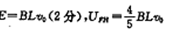
小题2:见解析
小题3: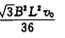
本题解析:
本题难度:一般
3、简答题 如图所示为某一装置的俯视图,M、N为两个竖直放置的平行金属板,相距为0.4 m,L1和L2为与M、N平行的两根金属导轨(两导轨较细,与M、N上边棱处于同一水平面),L1与M以及L2与N的间距都是0. 1 m,两导轨的电阻不计,其右端接有R="0." 3Ω的电阻.现有一长为0. 4 m、电阻为0.2Ω的均匀金属导体棒ab,棒上的a、b、c、d四点分别与M、 N、L1、L2接触良好,且金属棒ab与金属板M、N正交,整个装置放在竖直向下的匀强磁场中.今有一带正电粒子(不计重力)以v0="7" m/s的初速度平行于极板水平入射.求当金属棒ab向何方向以多大速度运动时,可使带电粒子做匀速直线运动?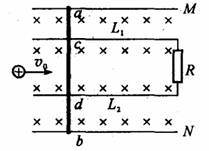
参考答案:金属棒ab应向右运动.且速度为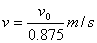
本题解析:金属棒ab应向右运动.设匀强磁场的磁感应强度为B,金属棒的运动速度为v.则金属棒c、d部分的感应电动势为 ,c、d两点间的内阻由电阻定律可得
,c、d两点间的内阻由电阻定律可得 Ω,c、d两点间的电势差为
Ω,c、d两点间的电势差为 。
。
两金属板M、N间的电势差为 ,
,
两板间的电场强度为E="0." 875Bv, 欲使带电粒子做匀速直线运动,应使粒子受力平衡,即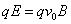 ,得
,得 m/s.
m/s.
本题难度:一般
4、计算题 如图甲所示,平行金属导轨竖直放置,导轨间距为L=1m,上端接有电阻R1=3Ω,下端接有电阻R2=6Ω,虚线OO′下方是垂直于导轨平面的匀强磁场.现将质量m=0.1kg、电阻不计的金属杆ab,从OO′上方某处垂直导轨由静止释放,杆下落0.2m过程中始终与导轨保持良好接触,加速度a与下落距离h的关系图象如图乙所示.求: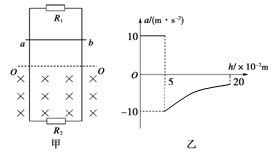
(1)磁感应强度B;
(2)杆下落0.2m过程中通过电阻R2的电荷量q.
参考答案:(1) 2T(2) 0.05C
本题解析:(1)由图象知,杆自由下落距离是0.05m,当地重力加速度g=10m/s2,则杆进入磁场时的速度v=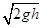 =1m/s
=1m/s
由图象知,杆进入磁场时加速度a=-g=-10m/s2
由牛顿第二定律得mg-F安=ma
回路中的电动势E=BLv
杆中的电流I=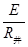
R并=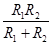
F安=BIL=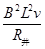
得B=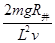 =2T
=2T
(2)杆在磁场中运动产生的平均感应电动势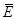 =
=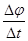
杆中的平均电流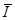 =
=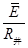
通过杆的电荷量Q=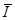 ·Δt
·Δt
通过R2的电量q=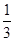 Q=0.05C
Q=0.05C
本题主要考查对电磁感应定律的应用,先根据图象得到杆进入磁场的速度,再根据牛顿定律求出磁场对杆的安培力,根据感应电动势和安培力的计算公式计算出磁感应强度,根据平均电流和时间计算出电荷量;
本题难度:困难
5、选择题 如图所示的4种情况中,磁场的磁感应强度都是B,导体的长度l和运动速度v的大小都相同.产生感应电动势最小的是(?)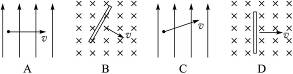
参考答案:C
本题解析:在这4种情况中,只由C项中导线速度方向不和磁感线方向垂直,故C项中的导线产生的感应电动势最小.
本题难度:简单