时间:2020-08-15 23:53:49
1、选择题 取一只扁玻璃瓶,里面盛满水,用穿有透明细管的橡皮塞封口,使水面位于细管中(如图).用手捏玻璃瓶,可以看到透明细管中的水面变化,这一实验的目的是( )
A.说明玻璃瓶中的水可以发生形变
B.说明玻璃瓶可以发生形变
C.验证弹力的大小跟形变量成正比
D.验证液体的流动性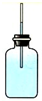
参考答案:B
本题解析:
本题难度:一般
2、选择题 (1)常用螺旋测微器的精度是 ,右图中的螺旋测微器读数为
,右图中的螺旋测微器读数为 ,请你在刻度线旁边的方框内标出相应的数以符合给出的数值。
,请你在刻度线旁边的方框内标出相应的数以符合给出的数值。
参考答案:)如右图(螺旋测微器的三个刻度线每个值1分。)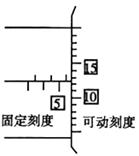
本题解析: ?可根据螺旋测微器读数结合题图可知,主尺固定刻度填5,这样主尺读取
?可根据螺旋测微器读数结合题图可知,主尺固定刻度填5,这样主尺读取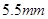 ,可动刻度应读取
,可动刻度应读取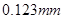 ,由于精度为
,由于精度为 ,故可动数据读取
,故可动数据读取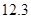 时,下面的方框填写10,上面的方框填写15
时,下面的方框填写10,上面的方框填写15
本题难度:简单
3、计算题 上表面光滑的木板MN上有一固定挡板,原长相同的两轻质弹簧k1、k2如图示与两质量均为m的小球A、B和固定挡板连接,当木板水平放置时,两弹簧均处于原长状态,缓慢抬起木板的N端,当木板与水平面成300时,k1、k2长度之比为6:7,当AB转至竖直时k1、k2长度之比为7:9,求:
(1)?k1、k2劲度系数之比
(2)?当AB转至竖直后,用竖直向上的力F轻推A,使A缓慢上升,直至k1、k2长度和等于两弹簧原长和,求此时力F的大小。(重力加速度g已知)
参考答案:(1)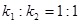 ?(2)
?(2)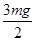
本题解析:木板倾斜30°角时,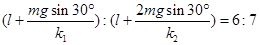 ?
?
木板竖直时, 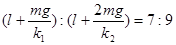
可解得: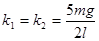 ,所以
,所以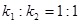 ?
?
当两弹簧长度和等于两弹簧原长和时,必然有一弹簧伸长、一弹簧压缩,且形变量大小一样,分析B球受力可知,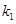 伸长、
伸长、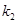 压缩(只要能体现两弹簧形变特征就给分)
压缩(只要能体现两弹簧形变特征就给分)
设此时两弹簧形变量均为x
对B球有: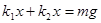
对A球有: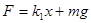
联立上述两式可解得: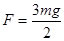
点评:本题难点是第(2)问,知道此种状态下那根弹簧伸长,那根弹簧被压缩,分别对两球列力的平衡表达式求解。
本题难度:一般
4、实验题 (9分每小题3分)在《验证牛顿第二定律》的实验中,图为实验装置示意图。 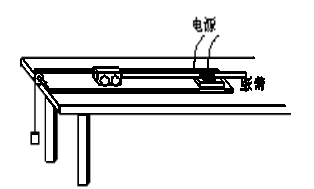
(1)除图中所示仪器外,还需要下列哪些仪器? (?)
A.?天平?B.秒表? C.带毫米刻度的刻度尺 ?D.弹簧测力计? E.低压交流电源 ?F.低压直流电源
(2)为了保证实验条件和减小误差,以下哪些措施是必要的??(?)?
A.每次改变小车的质量后,需要重做平衡摩擦力的工作
B.将木板的一端垫高,使小车不受拉力时恰能在木板上做匀速运动
C.尽量使沙与沙桶的总质量比小车质量小得多
D.同一条件下多打几条纸带
(3)某学生在平衡摩擦力时,把长木板的一端垫得过低,使得倾角偏小。他所得到的a-F关系可用图中哪条图线表示?(图中a是小车的加速度,F是细线作用于小车的拉力)答:?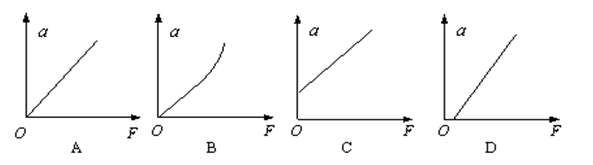
参考答案:(1)(ACE)? (2)(?BCD)? (3)?D
本题解析:根据测量需要,需要知道砝码的重量,所以要填平,打点计时器要工作需要低压交流电源,为了测量加速度还需要刻度尺,ACE。为了减少误差,需要满足小车质量远远大于沙桶及沙的质量,并要尽量减少摩擦力,为了让加速度更准确,需要多打一些纸袋,所以BCD。由于摩擦力没有平衡完毕,所以不会过坐标原点,即为D。
点评:此类题型考察了验证本实验中的一些细节。对实验的处理,例如摩擦力如何平衡,图像如何处理等
本题难度:一般
5、实验题 请读出游标卡尺的数值? .mm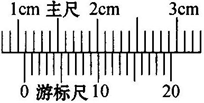
参考答案:10.55
本题解析:游标卡尺读数的方法是主尺读数加上游标读数,不需估读.
解答:解:游标卡尺,主尺读数为10mm,游标读数为0.1×11mm=0.55mm,所以最终读数为10.55.
故本题答案为10.55.
点评:解决本题的关键掌握游标卡尺的读数方法,游标卡尺读数的方法是主尺读数加上游标读数,不需估读.
本题难度:简单