时间:2020-08-15 23:15:43
1、计算题 如图所示,两根相同的劲度系数为k的金属轻弹簧用两根等长的绝缘线悬挂在水平天花板上,弹簧的上端通过导线与阻值为R的电阻相连,弹簧的下端接一质量为m、长度为L、电阻为r的金属棒,金属棒始终处于宽度为d的垂直纸面向里磁感应强度为B的匀强磁场中。开始时弹簧处于原长。金属棒从静止释放,其下降高度为h时达到了最大速度。已知弹簧始终在弹性限度内,且当弹簧的形变量为x时,它的弹性势能为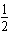 kx2,不计空气阻力和其他电阻,求:
kx2,不计空气阻力和其他电阻,求:
(1)金属棒的最大速度是多少?
(2)这一过程中R消耗的电能是多少? 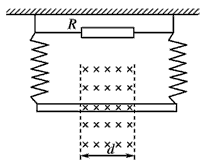
参考答案:解:(1)当金属棒有最大速度时,加速度为零,金属棒受向上的弹力、安培力和向下的重力作用,有
2kh+BId=mg
I=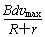
vmax=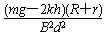
(2)根据能量关系得mgh-2×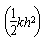 -
-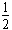 mvmax2=E电
mvmax2=E电
又有R、r共同消耗了总电能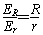 ,ER+Er=E电
,ER+Er=E电
整理得R消耗的电能为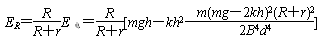
本题解析:
本题难度:困难
2、简答题 如图12.2-5,电阻不计的两条平行导轨间距为L,两端各接有阻值为R的电阻和电容为C的电容器.导轨平面竖直放置在与之垂直的磁感应强度为B的匀强磁场中金属杆ab长2L,a端与导轨绞接,其电阻不计.ab杆自竖直位置由静止开始绕a顺时针沿光滑的导轨平面倒下,当杆转过600角时角速度为ω,求整个倒下过程中通过R的电量.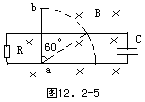
?
参考答案: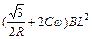
本题解析:当ab向右倒下且b端离开导轨前闭合电路中磁通量发生变化,R中有感应电流通过,接入回路中的旋转导体棒作为电源一方面对R供电,使电量q1流过R,另一方面又对C充电,充电电量逐渐增至q2;当b端离开导轨后,由于旋转导体棒脱离回路,充了电的C又对R放电,这样又有电量q2流过R,。通过R的电量应该是感应电流的电量和电容器放电的电量之和。1.通过R的感应电量q1=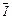 Δt=ΔΦ/R=
Δt=ΔΦ/R=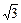 BL2/2R;2.通过R的电容器放电电量q2=CE=
BL2/2R;2.通过R的电容器放电电量q2=CE=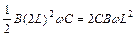 ,总电量q=q1+q2=
,总电量q=q1+q2=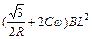
点评:本题要求能分析整个物理过程,合理选择感应电动势的平均值和瞬时值的表达式,另外考察导线转动切割的公式E=Bl2ω/2.
本题难度:一般
3、计算题 如图所示,半径为R的圆形导轨处在垂直于圆平面的匀强磁场中,磁感应强度为B,方向垂直于纸面向内。一根长度略大于导轨直径的导体棒MN以速率v在圆导轨上从左端滑到右端,电路中的定值电阻为r,其余电阻不计,导体棒与圆形导轨接触良好。求:
(1)在滑动过程中通过电阻r的电流的平均值;
(2)MN从左端到右端的整个过程中,通过r的电荷量;
(3)当MN通过圆导轨中心时,通过r的电流是多大?

参考答案:解:(1)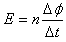 ,
, ,
,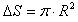 ,
,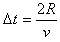
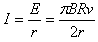
(2)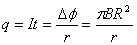
(3)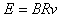
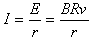
本题解析:
本题难度:困难
4、选择题 如图7-1,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aob(在纸面内),磁场方向垂直于纸面朝里,另有两根金属导轨c、d分别平行于oa、ob放置。保持导轨之间接触良好,金 属导轨的电阻不计。现经历以下四个过程:①以速度v移动d,使它与ob的距离增大一倍;②再以速率v移动c,使它与oa的距离减小一半;③然后,再以速率2v移动c,使它回到原处;④最后以速率2v移动d,使它也回到原处。设上述四个过程中通过电阻R的电量的大小依次为Q1、Q2、Q3和Q4,则(?)
A.Q1=Q2=Q3=Q4
B.Q1=Q2=2Q3=2Q4
C.2Q1=2Q2=Q3=Q4
D.Q1≠Q2=Q3≠Q4
参考答案:A
本题解析:设开始导轨d与Ob的距离为x1,导轨c与Oa的距离为x2,由法拉第电磁感应定律知移动c或d时产生的感应电动势:E= =
= ,通过R的电量为:Q=I=
,通过R的电量为:Q=I=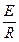 Δt=
Δt= 。可见通过R的电量与导体d或c移动的速度无关,由于B与R为定值,其电量取决于所围成面积的变化。①若导轨d与Ob距离增大一倍,即由x1变2x1,则所围成的面积增大了ΔS1=x1·x2;②若导轨c再与Oa距离减小一半,即由x2变为x2/2,则所围成的面积又减小了ΔS2=2x1·x2/2=x1·x2;③若导轨c再回到原处,此过程面积的变化为ΔS3=ΔS2=2x1·x2/2=x1·x2;④最后导轨d又回到原处,此过程面积的变化为ΔS4=x1·x2;由于ΔS1=ΔS2=ΔS3=ΔS4,则通过电阻R的电量是相等的,即Q1=Q2=Q3=Q4。
。可见通过R的电量与导体d或c移动的速度无关,由于B与R为定值,其电量取决于所围成面积的变化。①若导轨d与Ob距离增大一倍,即由x1变2x1,则所围成的面积增大了ΔS1=x1·x2;②若导轨c再与Oa距离减小一半,即由x2变为x2/2,则所围成的面积又减小了ΔS2=2x1·x2/2=x1·x2;③若导轨c再回到原处,此过程面积的变化为ΔS3=ΔS2=2x1·x2/2=x1·x2;④最后导轨d又回到原处,此过程面积的变化为ΔS4=x1·x2;由于ΔS1=ΔS2=ΔS3=ΔS4,则通过电阻R的电量是相等的,即Q1=Q2=Q3=Q4。
本题难度:简单
5、选择题 如图所示,两个垂直纸面的匀强磁场方向相反,磁感应强度的大小均为B,磁场区域的宽度均为2a,一个直径为2a的导线圆环从图示位置沿x轴正方向匀速穿过两磁场区域,以逆时针方向为电流的正方向,则感应电流I与导线圆环移动距离x的关系图象正确的是( ? )





参考答案:C
本题解析:
本题难度:一般