时间:2020-08-15 23:14:40
1、计算题 (18分)如图所示,在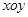 平面内的第一象限内存在沿
平面内的第一象限内存在沿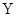 轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度
轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度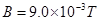 ,有一质量为
,有一质量为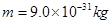 ,电量为
,电量为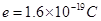 的电子以
的电子以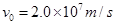 的速度从
的速度从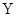 轴的
轴的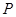 点(0,
点(0,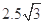 cm)沿
cm)沿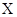 轴正方向射入第一象限,偏转后从
轴正方向射入第一象限,偏转后从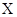 轴的
轴的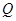 点射入第四象限,方向与
点射入第四象限,方向与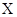 轴成
轴成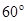 角,在磁场中偏转后又回到
角,在磁场中偏转后又回到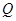 点,方向与
点,方向与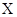 轴也成
轴也成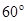 角;不计电子重力.求:
角;不计电子重力.求: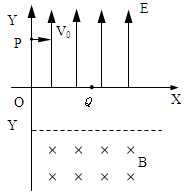
(1)OQ之间的距离及电子通过Q点的速度大小.
(2)若在第四象限内的磁场的边界为直线边界,即在虚线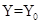 的下方有磁场,如图中所示,求
的下方有磁场,如图中所示,求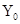 的坐标.
的坐标.
(3)若在第四象限内的磁场为圆形边界的磁场,圆形边界的磁场的圆心坐标的范围.
参考答案:(1)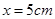 ,
,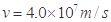 (2)
(2)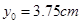 ?(3)
?(3)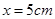 ,
,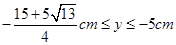
本题解析:
试题分析:(1)电子在电场做类平抛运动,从P到Q过程中,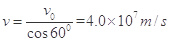 ?①
?①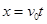 ?②?
?②?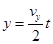 ?③?
?③?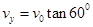 ?④
?④
解得: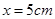 ?⑤
?⑤
(2)电子在磁场中做匀速圆周运动,故有: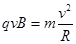 ?⑥
?⑥
由几何关系可知,电子回到Q点有: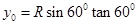 ?⑦
?⑦
解得: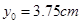 ?⑧
?⑧
(3)由于在磁场中偏转后又回到Q点,方向与X轴也成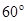 角.其运动轨迹如图:
角.其运动轨迹如图: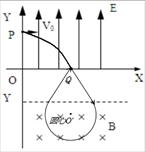
由几何关系可知,圆形磁场的圆心在Q点的正下方,即: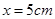
圆形磁场应与电子轨迹有公共弦,同时只要磁场半径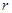 大于
大于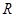 即可,故磁场圆心y轴的最小坐标为:
即可,故磁场圆心y轴的最小坐标为: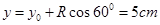
圆形磁场在第四象限,磁场半径应小于5cm,由几何关系可知,磁场圆心y轴的最大坐标为: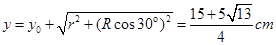
即圆形磁场的圆心的坐标应满足: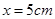 ,
,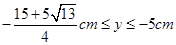
本题难度:一般
2、计算题 如图所示,在坐标系xOy第二象限内有一圆形匀强磁场区域(图中未画出),磁场方向垂直xOy平面。在x轴上有坐标(-2l0,0)的P点,三个电子a、b、c以相等大小的速度沿不同方向从P点同时射入磁场区,其中电子b射入方向为+y方向,a、c在P点速度与b速度方向夹角都是θ=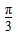 。电子经过磁场偏转后都垂直于y轴进入第一象限,电子b通过y轴Q点的坐标为y=l0,a、c到达y轴时间差是t0。在第一象限内有场强大小为E,沿x轴正方向的匀强电场。已知电子质量为m、电荷量为e,不计重力。求:
。电子经过磁场偏转后都垂直于y轴进入第一象限,电子b通过y轴Q点的坐标为y=l0,a、c到达y轴时间差是t0。在第一象限内有场强大小为E,沿x轴正方向的匀强电场。已知电子质量为m、电荷量为e,不计重力。求:
(1)电子在磁场中运动轨道半径和磁场的磁感应强度B。
(2)电子在电场中运动离y轴的最远距离x。
(3)三个电子离开电场后再次经过某一点,求该点的坐标和先后到达的时间差Δt。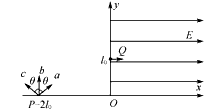
参考答案:解:(1)三电子轨迹如图。 
由图可知,R=l0
设a、c到达y轴时间差为t0,其中它们离开磁场后到达y轴时间是相等的,在磁场区中a转过30°圆心角,时间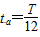 ,c转过150°圆心角,时间
,c转过150°圆心角,时间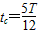 ,
,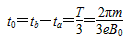
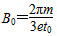
(2)电子在磁场中运动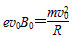
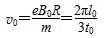
在电场中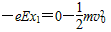
得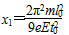 。
。
(3)电子离开电场再次返回磁场轨迹如图,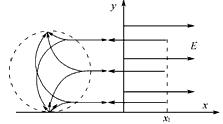
坐标x=-2l0,y=2l0,
由运动的对称性可知, a、c同时到达,与b比较磁场中运动时间都是半个周期,
电场中运动时间也都相等,所以时间差为在非场区 ,
,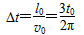 ,
,
b先到达。
本题解析:
本题难度:困难
3、选择题 不计重力的负粒子能够在如图所示的正交匀强电场和匀强磁场中匀速直线穿过.设产生匀强电场的两极板间电压为U,距离为d,匀强磁场的磁感应强度为B,粒子带电荷量为q,进入速度为v,以下说法正确的是( )
A.若同时增大U和B,其他条件不变,则粒子一定能够直线穿过
B.若同时减小d和增大v,其他条件不变,则粒子可能直线穿过
C.若粒子向下偏,能够飞出极板间,则粒子动能一定减小
D.若粒子向下偏,能够飞出极板间,则粒子的动能有可能不变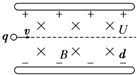
参考答案:A、若同时增大U和B,其他条件不变,虽然使得电场力与洛伦兹力均增大,但两者不一定相等,所以粒子可能做直线运动,也可能做曲线运动,故A错误;
B、若同时减小d和增大v,其他条件不变,则会有电场力与洛伦兹力均增大,但两者不一定相等,所以粒子可能做直线运动,故B正确;
C、若粒子向下偏,能够飞出极板间,则电场力做负功,由于洛伦兹力不做功,所以导致动能一定减小.故C正确;
D、若粒子向下偏,能够飞出极板间,则电场力做负功,由于洛伦兹力不做功,所以导致动能一定减小.故D错误;
故选:BC
本题解析:
本题难度:简单
4、计算题 在如图a所示的空间里,存在方向水平垂直于纸面向里的匀强磁场和竖直向上的周期性变化的电场(如图b所示),周期T=12t0,电场强度的大小为E0,E>0表示电场方向竖直向上。一倾角为300足够长的光滑绝缘斜面放置在此空间。t=0时,一带负电、质量为m的微粒从斜面上的A点由静止开始沿斜面运动,到C点后,做一次完整的圆周运动,在t=T时刻回到C点,再继续沿斜面运动到t=13t0时刻。在运动过程中微粒电荷量不变,重力加速度为g,上述E0、m、t0、g为已知量。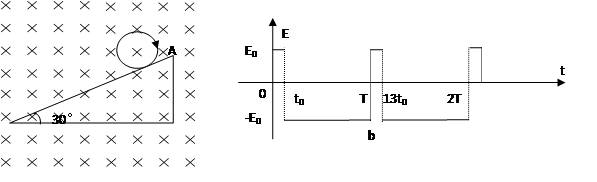
(1)求微粒所带电荷量q和磁感应强度大小B;
(2)求微粒在A、C间运动的加速度和运动到C点时的速度大小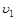 ;
;
(3)求0~2T时间内微粒经过的路程。
参考答案:(1)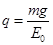 ?
?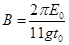 (2)
(2)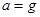 ,方向沿斜面向下;
,方向沿斜面向下;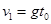 (3)
(3)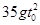
本题解析:(1)能够做匀速圆周运动,说明此时重力和电场力合力为零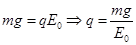
设粒子达到C点时的速度为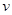 ,洛伦兹力提供向心力,有
,洛伦兹力提供向心力,有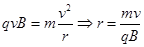
运动的周期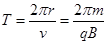
在本题中圆周运动的周期为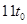 ,则
,则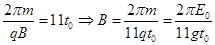
(2)微粒在AC间运动时受力分析如图所示,则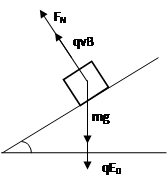
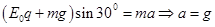 ,方向沿斜面向下
,方向沿斜面向下
到达C点时速度大小为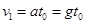
(3)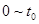 时间内路程
时间内路程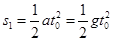
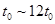 时间内的路程
时间内的路程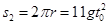
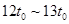 时间内的路程
时间内的路程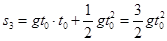
第二次做圆周运动的速度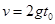 ,半径是第一次的两倍
,半径是第一次的两倍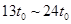 时间内的路程
时间内的路程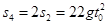
所以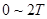 时间内的总路程为
时间内的总路程为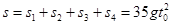
点评:本题要弄清带电粒子在各个时间段的运动情况,逐段分析求解。
本题难度:一般
5、填空题 如图所示是电磁流量计的示意图。圆管由非磁性材料制成、空间有匀强磁场。当管中的导电液体流过磁场区域时,测出管壁上MN两点间的电势差为E,就可以知道管中流体的流量q
参考答案:
本题解析:
本题难度:一般