时间:2020-08-15 23:00:07
1、计算题 如图所示,两个带电滑块甲和乙系于一根绝缘细绳的两端,放在一个光滑的绝缘平面上,整体置于方向水平向右、大小为 N/C的匀强电场中,甲的质量为
N/C的匀强电场中,甲的质量为 kg,带电荷量为
kg,带电荷量为 C,乙的质量为
C,乙的质量为 kg,带电荷量为
kg,带电荷量为 C。开始时细绳处于拉直状态。由静止释放两滑块,t=3s时细绳断裂,不计滑块间的库仑力。试求:
C。开始时细绳处于拉直状态。由静止释放两滑块,t=3s时细绳断裂,不计滑块间的库仑力。试求:
(1)细绳断裂前,两滑块的加速度;
(2)由静止开始释放后的整个运动过程中,乙的电势能增量的最大值;
(3)当乙的电势能增量为零时,甲与乙组成的系统机械能的增量。
参考答案:(1)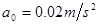 (2)
(2)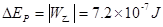 (3)
(3)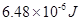
本题解析:(1)取水平向右为正方向,将甲乙及细绳看作一个整体,根据牛顿第二定律: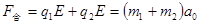
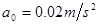
(2)当乙发生的位移最大时,乙的电势能增量最大
细绳断裂前,甲乙发生的位移均为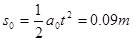
细绳断裂后,乙物体的加速度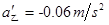 ,初速度
,初速度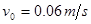
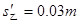 ,
,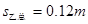 ,
,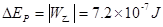
(3)当乙的电势能增量为零时,即乙回到了出发点,设绳子断裂后乙经过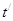 回到了出发点
回到了出发点 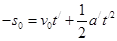 求得
求得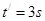
细绳断裂后,甲的加速度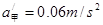
甲继续发生的位移为
当乙回到出发位置时甲的总位移 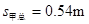 (2分)
(2分)
电场力对甲做的功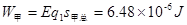 (2分)
(2分)
所以系统的机械能增量为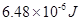
考点:本题考查牛顿第二定律、功能量守恒
本题难度:一般
2、选择题 两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连。A静止于水平地面上,如图所示。不计摩擦,A对绳的作用力的大小与地面对A的作用力的大小分别为 
A.mg,(M-m)g
B.mg,Mg
C.(M-m)g,mg
D.(M+m)g,(M-m)g
参考答案:A
本题解析:以B为研究对象知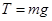 ,对A有
,对A有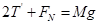 ,
,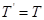 ,得
,得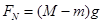 ,A对。
,A对。
本题难度:一般
3、选择题 如图所示:一个质量为M的倒“日”字木框中间套有一质量为m的圆环静止放在水平面上,现给圆环一向上初速度V,当圆环向上运动过程中,木框恰好对地面无压力,则此时圆环的加速度为( )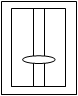
A 0 B g C Mg/m D (m+M)g/m
参考答案:D
本题解析:分析:(1)对木框进行受力分析,木框恰好对地面无压力,所以木框受到重力和圆环对它向上的摩擦力,合力等于零;
(2)对圆环进行受力分析,它受到重力和向下的摩擦力,根据牛顿第二定律即可求出其加速度.
解答:解:木框恰好对地面无压力,所以Mg=f
对圆环进行受力分析,根据牛顿第二定律得: mg+f=ma
a=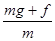 =
=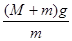
故选D.
点评:本题是牛顿第二定律的直接应用,解题的关键是正确对木框和圆环进行受力分析.
本题难度:一般
4、选择题 如图所示,两个用轻线相连的位于光滑水平面上的物块,质量分别为m1和m2.拉力F1和F2方向相反,与轻线沿同一水平直线,且F1 > F2,试求在两个物块运动过程中轻线的拉力T的大小为( ).
A.F1+F2
B.
C.
D.
参考答案:D
本题解析:据牛顿第二定律,由于水平面是光滑的,在水平方向两个物体都只受到拉力F1、F2,在拉力作用下两个物体一起做匀加速直线运动,两个物体的加速度相等,则由整体法:F1-F2=(m1+m2)a,得a= (F1-F2)/( m1+m2);将m1隔离,得F1-T= m1a,则T=  ,所以D选项正确。
,所以D选项正确。
考点:本题考查牛顿第二定律的应用。
本题难度:一般
5、选择题 如图所示,静止在光滑水平面上的物体A,一端靠着处于自然状态的弹簧.现对物体作用一水平恒力,在弹簧被压缩到最短的过程中,物体的速度和加速度的变化情况是 
A.速度增大,加速度增大
B.速度增大,加速度减小
C.速度先增大后减小,加速度先增大后减小
D.速度先增大后减小,加速度先减小后增大
参考答案:D
本题解析:在弹簧压缩过程中,弹簧的弹力从零开始增加,所以开始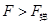 ,根据牛顿第二定律可得
,根据牛顿第二定律可得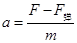 ,合力向左,加速度向左,因为A向左运动,所以A做加速运动,由于随着A向左运动的雾位移增大,所以弹簧压缩量增大,弹力增大,所以加速度减小,故A做加速度减小的加速运动;当
,合力向左,加速度向左,因为A向左运动,所以A做加速运动,由于随着A向左运动的雾位移增大,所以弹簧压缩量增大,弹力增大,所以加速度减小,故A做加速度减小的加速运动;当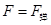 时,加速度为零,速度达到最大,之后
时,加速度为零,速度达到最大,之后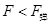 ,合力向右,加速度向右,而A继续向左运动,所以A做减速运动,并且随着弹力的增大,加速度在增大,故A做加速度增大的减速运动,综上所述A的速度先增大后减小,加速度先减小后增大,D正确;
,合力向右,加速度向右,而A继续向左运动,所以A做减速运动,并且随着弹力的增大,加速度在增大,故A做加速度增大的减速运动,综上所述A的速度先增大后减小,加速度先减小后增大,D正确;
考点:考查了牛顿第二定律的瞬时性
本题难度:一般