时间:2020-08-15 22:56:14
1、实验题 (1)以下四幅照片中“用DIS测变速直线运动瞬时速度”的实验装置图是__________;
(2)“用DIS测定加速度”的实验装置图是________。(选填照片下对应的字母) 

(3)在“用DIS测定加速度”的实验中,下列说法正确的是________。?
A.?可以使用A图实验装置,直接用s-t图像处理数据
B.?可以使用C图实验装置,将测得的数据,通过数据采集器和计算机转化为v-t图像
C.?可以使用C图实验装置,直接得到加速度随时间变化的图像
D.?可以使用D图实验装置,通过图象分析物体在运动过程中速度的变化情况?
2、计算题 升降机由静止开始以加速度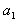 匀加速上升
匀加速上升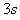 ,速度达到
,速度达到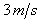 ,接着匀速上升
,接着匀速上升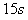 ,最后再以加速度
,最后再以加速度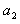 匀减速上升
匀减速上升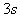 才停下来,整个过程中升降机升高了54m。求:
才停下来,整个过程中升降机升高了54m。求:
(1)匀加速上升的加速度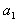 ;
;
(2)匀减速上升的加速度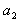 ;
;
(3)整个过程中升降机的平均速度大小。
3、选择题 物体做变速直线运动,加速度大小恒为2m/s2,就是说( )
A.物体速度的变化量为2m/s
B.任意1s内末速度都是初速度的2倍
C.在任意1s内,物体的初速度可能比末速度大2m/s
D.运动过程中任意时刻的瞬时速度比1s前的瞬时速度增加2m/s
4、选择题 长为1m的细线一端系一个质量为1kg的小球,用力推一下小球,使它绕细线的另一端在竖直平面内做圆周运动,则(重力加速度为10m/s2)
[? ]
A.小球可能做匀速圆周运动
B.小球在最高点时的速率可为2m/s
C.小球在最高点的速率可为5m/s
D.小球在最低点时细线的拉力可为10N
5、选择题 如图所示,放于竖直面内的光滑金属圆环半径为R,质量为m的带孔小球穿于环上,同时有一长为R的细绳一端系于圆环最低点.当圆环以角速度ω绕竖直直径转动时,发现小球受到三个力作用.
则ω可能为( )
A.
B.
|