时间:2020-08-15 22:34:20
1、简答题 弹性小球从某一高度H自由下落到水平地面上,与水平地面碰撞后弹起,假设小球与地面的碰撞过程中没有能量损失,但由于受到大小不变的空气阻力的影响,使每次碰撞后弹起上升的高度是碰撞前下落高度的
| 3 4 |
| 3 4 |
| 1 4 |
| 1 2 |
| 1 4 |
|
参考答案:不同意,该学生只考虑小球回到34H后要继续上升所需克服重力做功的动能,忽略了继续上升时还要有能量克服空气阻力做功.?
正确的解法是:
根据动能定理得:WG+Wf=△Ek
对第一种情况的整个过程:14mgH-74fH=0
得空气阻力大小为:f=17mg
对第二情况:Wf=0-12mv20
即:-2fH=0-12mv20
则得:17mg2H=12mv20
解得:v0=
本题解析:
本题难度:一般
2、选择题 甲、乙两物体在同一地点分别从4h和h高处开始做自由落体运动,已知甲物体的质量是乙物体的4倍,下列说法正确的是( )
A.落地时,甲和乙的速度相等
B.落地时,甲的速度是乙的速度的2倍
C.甲、乙同时落地
D.甲的下落时间是乙的下落时间的4倍
参考答案:A、由于高度不同,则有v2=2gh可知,落地时速度不相等,故A错误;
B、由v2=2gh得v=
本题解析:
本题难度:一般
3、填空题 物体从某一高度自由下落,整个过程中中间时刻速度是10m/s,则物体是从高______m处下落,下落时间为______s.
(g=10m/s2)
参考答案:根据v=gt得:
t=vg=1010s=1s
所以运动的总时间为2s
根据h=12gt2
得h=12×10×4m=20m
故答案为:20;2
本题解析:
本题难度:一般
4、计算题 据报道,三岁小童闹闹玩耍时不慎从45m高的阳台上无初速掉下,在他刚掉下时恰被楼下一管理人员发现,该人员迅速由静止冲向闹闹下落处的正下方楼底,准备接住闹闹。已知管理人员到闹闹下落处的正下方楼底的距离为15m,为确保安全稳妥地接住闹闹,管理人员将尽力节约时间,但又必须保证接闹闹时没有水平方向的冲击(即水平速度为零)。不计空气阻力,将儿童和管理人员都看做质点,设管理人员奔跑过程中只做匀速或匀变速运动(g取10m/s2)。问:
(1)管理人员至少用多大的平均速度跑到楼底?
(2)若管理人员在加速或减速过程的加速度大小相等,且最大速度不超过7.5m/s,求管理人员奔跑时至少需要多大的加速度?
参考答案:(1)5m/s? (2)7.5m/s2
本题解析:(1)儿童掉下做自由落体运动,可以通过自由落体的位移公式求出时间,根据时间再求管理员的最小平均速度.
(2)管理员先加速到速度最大,再匀速,再减速到0,抓住三段时间和等于自由落体的时间,三段位移和等于管理员到楼底的距离,求出最小加速度.
解:(1)儿童下落的时间为t,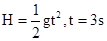
他要能接住儿童,奔跑的时间要小于3s
由x=vt,v=5m/s,故管理员的平均速度至少为6m/s.
(2)设管理员的加速度为a
时间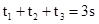
位移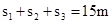
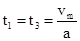 ,
,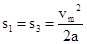 ,
,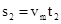
由上可得a=7.5m/s2
故加速度应满足a≥7.5m/s2.
点评:解决本题的关键抓住小孩自由下落的时间和管理员运动的时间相等,灵活运用运动学公式求解.
本题难度:简单
5、填空题 某一物体从某一高处自由下落,第1s内的位移为______m,第2s末的速度是______m/s,前3s内的平均速度为______m/s.(物体没有落地时)
参考答案:第1s内的位移x1=12gt12=12×9.8×1m=4.9m
第2s末的速度v2=gt2=9.8×2m/s=19.6m/s
前3s的位移为:x3=12gt32=12×9.8×9m=44.1m
所以前3s内的平均速度为.v=x3t3=44.13m/s=14.7m/s
故答案为:4.9,19.6,14.7.
本题解析:
本题难度:简单