时间:2020-08-09 23:51:24
1、简答题 在平面直角坐标系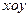 内,第一、第三象限有大小相等、垂直平面朝里的匀强磁场,第二象限有平行于平面沿-
内,第一、第三象限有大小相等、垂直平面朝里的匀强磁场,第二象限有平行于平面沿-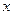 方向的匀强电场E2?,第四象限有平行于平面沿+
方向的匀强电场E2?,第四象限有平行于平面沿+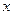 方向的匀强电场E1。一质量为
方向的匀强电场E1。一质量为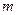 ,电量为-
,电量为-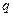 的带电粒子(不计重力),从
的带电粒子(不计重力),从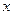 轴上的(
轴上的(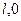 )点以速度
)点以速度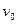 沿-
沿-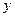 方向进入第四象限的电场中,后由
方向进入第四象限的电场中,后由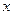 轴上的某点
轴上的某点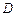 沿+
沿+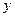 方向进入第二象限的电场中,最后从
方向进入第二象限的电场中,最后从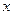 轴上的某点
轴上的某点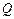 沿-
沿-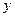 方向再度进入第四象限。已知
方向再度进入第四象限。已知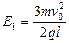 ,
,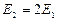 。求
。求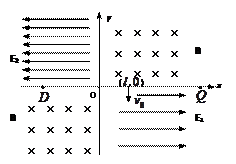
(1)磁感应强度B的大小
(2)带电粒子从第一象限进入第四象限时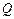 点的坐标
点的坐标
(3)带电粒子第一次经过全部四个象限的时间
2、简答题 已知如图,水平放置的平行金属板间有匀强电场。一根长l的绝缘细绳一端固定在O点,另一端系有质量为m并带有一定电荷的小球。小球原来静止在C点。当给小球一个水平冲量后,它可以在竖直面内绕O点做匀速圆周运动。若将两板间的电压增大为原来的3倍,求:要使小球从C点开始在竖直面内绕O点做圆周运动,至少要给小球多大的水平冲量?在这种情况下,在小球运动过程中细绳所受的最大拉力是多大?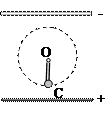
3、简答题 如图所示,在相互垂直的水平匀强电场和水平匀强磁场中,有一竖直固定绝缘杆 ,小球P套在杆上,已知P的质量为
,小球P套在杆上,已知P的质量为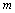 ,电荷量为
,电荷量为 ,P与杆间的动摩擦因数为
,P与杆间的动摩擦因数为 ,电场强度为
,电场强度为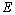 ,磁感应强度为
,磁感应强度为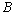 ,小球由静止起开始下滑,设电场、磁场区域足够大,杆足够长,求:
,小球由静止起开始下滑,设电场、磁场区域足够大,杆足够长,求:
(1)当下滑加速度为最大加速度一半时球的速度;
(2)当下滑速度为最大下滑速度一半时球的加速度。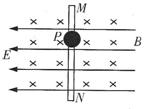
4、选择题 如图所示为一种获得高能粒子的装置,环形区域内存在垂直纸面向外、大小可调节的均匀磁场,质量为m,电量+q的粒子在环中做半径为R的圆周运动,A、B为两块中心开有小孔的极板,原来电势都为零,每当粒子顺时针飞经A板时,A板电势升高为U,B板电势仍保持为零,粒子在两板间电场中得到加速,每当粒子离开B板时,A板电势又降为零,粒子在电场一次次加速下动能不断增大,而绕行半径不变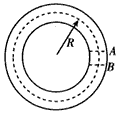
[? ]
A.粒子从A板小孔处由静止开始在电场作用下加速,绕行n圈后回到A板时获得的总动能为2nqU
B.在粒子绕行的整个过程中,A板电势可以始终保持为+U
C.在粒子绕行的整个过程中,每一圈的周期不变
D.为使粒子始终保持在半径为R的圆轨道上运动,磁场必须周期性递增,则粒子绕行第n圈时的磁感应强度为
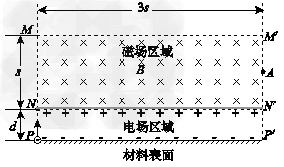
5、计算题 某仪器用电场和磁场来控制电子在材料表面上方的运动,如图所示,材料表面上方矩形区域PP"N"N充满竖直向下的匀强电场,电场宽为d;矩形区域NN"M"M充满垂直纸面向里的匀强磁场,磁感应强度为B,长为3s,宽为s;NN"为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子,从P点开始被电场加速经隔离层垂直进入磁场,电子每次穿越隔离层,时间极短、运动方向不变,其动能损失是每次穿越前动能的10%,最后电子仅能从磁场边界M"N"飞出。不计电子所受重力。
(1)控制电子在材料表面上方运动,最大的电场强度为多少?
(2)若电子以上述最大电场加速,经多长时间将第三次穿越隔离层?
(3)A是M"N"的中点,若要使电子在A、M"间垂直于AM"飞出,求电子在磁场区域中运动的时间。