时间:2020-08-09 23:38:37
1、计算题 有一种“双聚焦分析器”质谱仪,工作原理如图所示。加速电场的电压为U,静电分析器中有辐向会聚电场,即与圆心O1等距各点的电场强度大小相同,方向沿径向指向圆心O1;磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,其左边界与静电分析器的右边界平行.由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的电场方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器.而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器.测量出Q点与圆心O2的距离为d,位于Q点正下方的收集器入口离Q点的距离为d/2.(题中的U、m、q、R、d都为已知量)
(1)求静电分析器中离子运动轨迹处电场强度E的大小;
(2)求磁分析器中磁感应强度B的大小;
(3)现将离子换成质量为4m ,电荷量仍为q的另一种正离子,其它条件不变.磁分析器空间足够大,离子不会从圆弧边界射出,收集器的位置可以沿水平方向左右移动,要使此时射出磁分析器的离子仍能进入收集器,求收集器水平移动的距离.
参考答案:(1)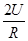 ; (2)
; (2)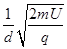 ?;(3)
?;(3)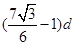
本题解析:(1)离子经电场直线加速,由动能定理: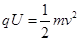
离子在静电分析器中做匀速圆周运动,根据牛顿第二定律,有: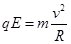
联立解得: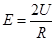
(2)离子在磁分析器中做匀速圆周运动,根据牛顿第二定律,有: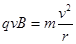
由题意可知,圆周运动的轨道半径: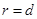
解得: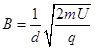
(3)另一正离子经电场加速后的速度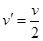
可得磁场中运动的半径为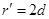
水平向右移动的距离为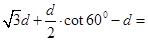
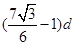
本题难度:一般
2、计算题 如图,相距为R的两块平行金属板M、N正对放置,s1、s2分别为M、N板上的小孔,s1、s2、O三点共线且水平,且s2O=R。以O为圆心、R为半径的圆形区域内存在大小为B、方向垂直纸面向外的匀强磁场。收集板D上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板。质量为m、带电量为+q的粒子,经s1无初速进入M、N间的电场后,通过s2进入磁场。粒子重力不计。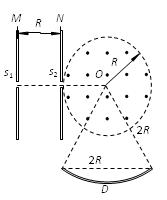
【小题1】若粒子恰好打在收集板D的中点上,求M、N间的电压值U;
【小题2】求粒子从s1到打在D的最右端经历的时间t。
参考答案:
【小题1】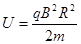
【小题2】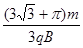
本题解析:(1)粒子从s1到达s2的过程中,根据动能定理得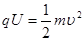 …………………… ①(2分)
…………………… ①(2分)
粒子进入磁场后在洛伦兹力作用下做匀速圆周运动,有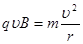 ………………………②(2分)
………………………②(2分)
当粒子打在收集板D的中点时,粒子在磁场中运动的半径r0=R……(2分)
解得: 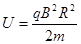 …………………………………………………(2分)
…………………………………………………(2分)
(2)根据几何关系可以求得粒子在磁场中运动的半径
r=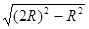 =
=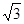 R ……………………………………………(2分)
R ……………………………………………(2分)
由 ②得粒子进入磁场时速度的大小 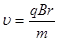 …………………………………………………(1分)
…………………………………………………(1分)
粒子在电场中经历的时间 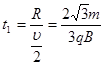 …………………………………………………(2分)
…………………………………………………(2分)
粒子在磁场中经历的时间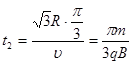 ……………………………………………(2分)
……………………………………………(2分)
粒子出磁场后做匀速直线运动经历的时间 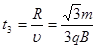 …………………………………………………(2分)
…………………………………………………(2分)
粒子从s1到打在收集板D上经历的最短时间为
t= t1+ t2+ t3=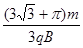 …………………………………………(1分)
…………………………………………(1分)
本题难度:一般
3、填空题 正方形导线框abcd,匝数为10匝,边长为20cm,在磁感强度为0.2T的匀强磁场中围绕与B方向垂直的转轴匀速转动,转速为120 r/min。当线框从平行于磁场位置开始转过90°时,线圈中磁通量的变化量是____wb,平均感应电动势为____V。
参考答案:0.008.? 0.64
本题解析:当线框从平行于磁场位置开始转过90°时,线圈中磁通量的变化量是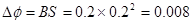 wb,平均感应电动势
wb,平均感应电动势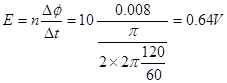
故答案为:0.008? 0.64
本题难度:简单
4、计算题 如图甲所示,竖直放置的金属板A、B中间开有小孔,小孔的连线沿水平放置的金属板C、D的中轴线,粒子源P可以连续地产生质量为m、电荷量为q的带正电粒子(初速不计),粒子在A、B间被加速后,再进入金属板C、D间偏转并均能从此电场中射出.已知金属板A、B间的电压UAB=U0,金属板C、D长度为L,间距d = .两板之间的电压UCD随时间t变化的图象如图乙所示.在金属板C、D右侧有一个垂直纸面向里的匀强磁场分布在图示的半环形带中,该环形带的内、外圆心与金属板C、D的中心O点重合,内圆半径Rl = .磁感应强度B0 =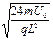 .已知粒子在偏转电场中运动的时间远小于电场变化的周期(电场变化的周期T未知),粒子重力不计.
.已知粒子在偏转电场中运动的时间远小于电场变化的周期(电场变化的周期T未知),粒子重力不计.
(1)求粒子离开偏转电场时,在垂直于板面方向偏移的最大距离;
(2)若所有粒子均不能从环形磁场的右侧穿出,求环形带磁场的最小宽度;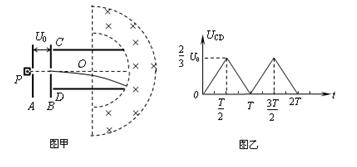
参考答案:(1)设粒子进入偏转电场瞬间的速度为v0,
对粒子加速过程由动能定理得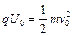 ? 3分
? 3分
进入偏转电场后,加速度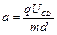 ? 1分
? 1分
设运动时间为t,则有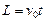 ? 1分
? 1分
只有t=T/2时刻进入偏转电场的粒子,垂直于极板方向偏移的距离最大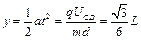 ?3分
?3分
(2)t =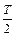 时刻进入偏转电场的粒子刚好不能穿出磁场时的环带宽度为磁场的最小宽度.设粒子进入磁场时的速度为v,
时刻进入偏转电场的粒子刚好不能穿出磁场时的环带宽度为磁场的最小宽度.设粒子进入磁场时的速度为v,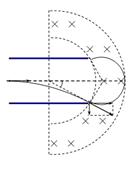
对粒子的偏转过程有 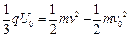 ?2分
?2分
解得 ? 1分
? 1分
在磁场中做圆周运动的半径为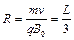 ? 2分
? 2分
如图所示,设环带外圆半径为R2,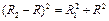 ? 2分
? 2分
解得R2="L?" 2分
所求d= R2-R1 = ? 1分
? 1分
本题解析:略
本题难度:一般
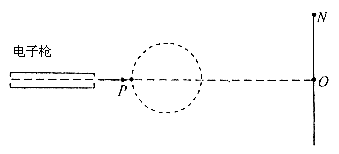
5、简答题 电视机的显像管中,电子束的偏转是用磁偏转技术实现的。在电子枪中产生的
电子经过加速电场加速后射出,从P点进入并通过圆形区域后,打到荧光屏上,如图所示。如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点。已知ON=h,PO=L。电子的电荷量为e,质量为m。求:
(1)电子打到荧光屏上的N点时的动能是多少?说明理由。
(2)电子在电子枪中加速的加速电压是多少?
(3)电子在磁场中做圆周运动的半径R是多少?
(4)试推导圆形区域的半径r与R及h、L的关系式。
 |
参考答案:(1)E?(2)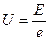 (3)
(3)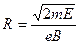 (4)
(4)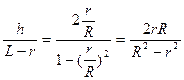
本题解析:(1)电子经过偏转磁场时洛伦兹力不做功,电子的动能仍为E。
(2)电子在电子枪中加速, ,加速电压为
,加速电压为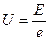 。
。
(3)电子从电子枪中射出的速度为 ,它做圆周运动的半径
,它做圆周运动的半径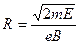 。
。
(4)如图所示,电子在偏转磁场中做圆周运动的圆心为O1,圆形区域的圆心为O2。 ?
?
电子从磁场圆射出时的速度方向与O2O的夹角设为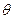 ,有
,有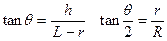
由半角公式可得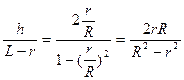 。
。
本题难度:一般