时间:2020-08-09 23:31:27
1、选择题 如所示，一细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球．当滑块以a=2g的加速度向左运动时，线中拉力T等于多少？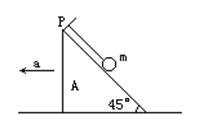
参考答案：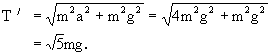
本题解析：根据小球贴着滑块运动时的受力情况，可列出水平方向和竖直方向的运动方程分别为
Tcos45°-Nsin45°=ma， ①
Tsin45°+Ncos45°=mg． ? ②
联立两式，得N=mgcos45°-masin45°．
若小球对滑块的压力等于零，即应使N=0，滑块的加速度至少应为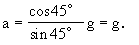
可见，当滑块以a=2g加速向左运动时，小球已脱离斜面飘起．此时小球仅受两个力作用：重力mg、线中拉力T′（图3-40）．设线与竖直方向间夹角为β．同理由牛顿第二定律得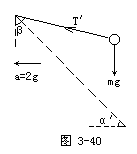
T′sinβ=ma，
T′cosβ=mg．
联立两式得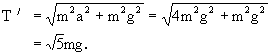
本题难度：一般
2、简答题 如图所示，质量为m的小木块A，放在质量为M的木板B的左端，B在水平拉力的作用下眼水平地面匀速向右运动，且A、B相对静止．某时刻撤去水平拉力，经过一段时间，B在地面上滑行了一段距离s，A在B上相对于B向右滑行了一段距离L后，A和B都停下．已知木板足够长，A、B间的动摩擦因数为μ1，B与地面间的动摩擦因数为μ2，且μ1＜μ2，求撤去水平拉力后：
（1）小木块和木板各自的加速度；
（2）小木块和木板滑行时间之比；
（3）木板B移动距离s的表达式．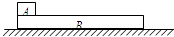
参考答案：（1）根据牛顿第二定律得，aA=μ1g?
aB=μ2(M+m)g-μ1mgM
（2）因为A、B的初速度相等，末速度为零，根据v=at知，时间之比等于加速度之反比．
t1t2=μ2(M+m)g-μ1mgμ1Mg
（3）对A应用动能定理-f1（L+s）=0-12mv2
对B应用动能定理 μ1mgs-μ2（m+M）gs=0-12Mv2
解得：消去v解得s=μ1ML(μ2-μ1)(M+m)．
答：（1）小木块和木板各自的加速度分别为aA=μ1g，aB=μ2(M+m)g-μ1mgM．
（2）小木块和木板滑行时间之比t1t2=μ2(M+m)g-μ1mgμ1Mg．
（3）木板B移动距离s的表达式s=μ1ML(μ2-μ1)(M+m)．
本题解析：
本题难度：一般
3、选择题 已知某质点做初速为零的匀变速直线运动，第3s内的位移大小为2.5m，则该质点前5s内的位移大小是多少（?）
A．25m
B．9m
C．12.5m
D．50m
参考答案：C
本题解析：前2s的位移为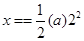
，前3s的位移为
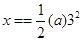，所以加速度为1m/s2，根据
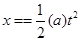可知可知，前5s位移应该为12.5m，答案为C
点评：此类题型考察了匀变速直线运动规律，在求第3s的位移时可以通过前3s的位移减去前2s的位移求。
本题难度：简单
4、选择题 关于自由落体运动，下面说法正确的是?（?）
A．它是竖直向下，v0=0，a=g的匀加速直线运动
B．在开始连续的三个1s内通过的位移之比是1∶3∶5
C．在开始连续的三个1s末的速度大小之比是1∶2∶3
D．从开始运动起依次下落4.9cm、9.8cm、14.7cm，所经历的时间之比为1∶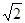
∶
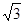
参考答案：ABC
本题解析：自由落体运动是初速度为零加速度为重力加速度的匀加速直线运动，A对；由初速度为零的匀加速直线运动的推论可知BC正确，从开始运动起依次下落第一个4.9cm、第二个4.9cm、第三个4.9cm、第四个4.9cm、第5个4.9cm、第6个4.9cm所通过的时间之比为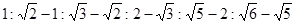
，可知从开始运动起依次下落4.9cm、9.8cm、14.7cm，所经历的时间之比为
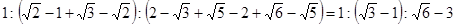，D错；
本题难度：简单
5、选择题 汽车以10m/s的速度在水平路面上做匀速直线运动，后来以2m/s2的加速度刹车，那么刹车后6s内的位移是（ ）
A．24 m
B．96 m
C．25 m
D．96 m或24 m
参考答案： C
本题解析：
试题分析: 根据公式可得，汽车静止时的时间为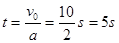
，故刹车后6s后的位移和5s时的位移相同，故为
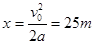，故C正确，A、B、D错误。
考点： 匀变速运动的位移
本题难度：一般