时间:2020-08-09 22:59:03
1、计算题 （14分）如左图，质量为0.5kg的物体受到与水平方向成37°拉力F的作用从静止开始做直线运动，一段时间后撤去拉力F，其运动的v－t图像如右图所示。已知cos37°=0.8，sin37°=0.6，g取10m/s2，求：
（1）物体与水平面间的动摩擦因数μ；
（2）拉力F的大小。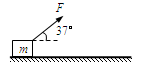
?
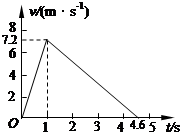
参考答案：（1）0.2；（2）5N
本题解析：（1）设撤去F时物体速度为v，由图象知，v=7.2m/s，
分析撤去F后物体的运动，
由图象知加速度的大小为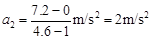
（2分）
由牛顿第二定律有：μmg=ma2
解得：μ=0.2（3分）
（2）分析在力F作用下物体的运动，
由图象知此段加速度大小为
（2分）
受力如图，由牛顿第二定律有：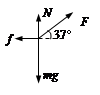
Fcos37°－f=ma1
N+Fsin37°=mg
又f=μN
由以上三式解得：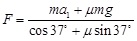
（5分）
代入数据得F=5N。（2分）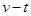
图象，物体受力分析
本题难度：一般
2、选择题 汽车以额定功率在平直公路上匀速行驶，在t1时刻司机减小了油门，使汽车的功率立即减小一半，并保持该功率继续行驶，到t2时刻汽车又开始做匀速直线运动（设整个过程中汽车所受的阻力不变）．则在t1～t2的这段时间内（ ）
A．汽车的加速度逐渐减小
B．汽车的加速度逐渐增大
C．汽车的速度先减小后增大
D．汽车的速度逐渐增大
参考答案：当汽车的功率减小一半，根据P=Fv知，此时牵引力减小为原来的一半，汽车做减速运动，速度减小，则牵引力增大，根据牛顿第二定律，知加速度减小，当牵引力增大到等于阻力时，又做匀速直线运动．知在t1～t2的这段时间内汽车的加速度逐渐减小，速度逐渐减小．故A正确，B、C、D错误．
故选A．
本题解析：
本题难度：一般
3、选择题 在光滑的水平面上有一质量为2kg的物体，它的左端与一劲度系数为l00N/m的轻弹簧相连，右端连接一细线，物体静止时细线与竖直方向成37°角，此时水平面对物体的弹力为零，如图所示．已知sin37°=0.6，cos37°=0.8，重力加速度g取10m/s2，则下列说法正确的是（ ）
A．当剪断弹簧的瞬问，物体的加速度为7.5m/s2
B．当剪断弹簧的瞬间，物体的合外力为15N
C．当剪断细线的瞬间，物体的加速度为零
D．当剪断细线的瞬间，物体受到的合外力为15N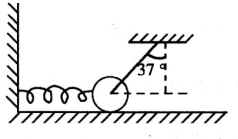
参考答案：A、B以物体为研究对象，进行受力分析可知，物体受细线拉力为T=25N，弹簧弹力为F=15N，在剪断弹簧的瞬间，细线的拉力会突变，物体静止不动，细线的拉力为0，加速度为0，故AB错误．
C、D在剪断细线的瞬间，弹簧的弹力不突变，受力分析可知，此时物体受到的合外力为15N，根据牛顿第二定律得：加速度为a=F合m=7.5m/s2．故C错误，D正确．
故选D
本题解析：
本题难度：简单
4、简答题 如图所示，两足够长的平行光滑的金属导轨MN、PQ相距为，导轨平面与水平面的夹角=30°，导轨电阻不计，磁感应强度为B的匀强磁场垂直于导轨平面向上．长为 的金属棒 垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量为、电阻为r=R．两金属导轨的上端连接一个灯泡，灯泡的电阻RL=R，重力加速度为g．现闭合开关S，给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F=mg的恒力，使金属棒由静止开始运动，当金属棒达到最大速度时，灯泡恰能达到它的额定功率．求：
（1）金属棒能达到的最大速度vm；
（2）灯泡的额定功率PL；
（3）金属棒达到最大速度的一半时的加速度a；
（4）若金属棒上滑距离为L时速度恰达到最大，求金属棒由静止开始上滑4L的过程中，金属棒上产生的电热Qr．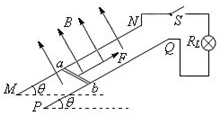
参考答案：（1）金属棒匀速运动时速度最大，则有F=mgsinθ+F安
又E=BLvm、I=ER+r=E2R、F安=BIL
联立解得，vm=2(F-mgsinθ)B2L2=2mg(1-sinθ)B2L2
（2）由上得?I=BLvm2R=mg(1-sinθ)BL
灯泡的额定功率为P=I2R=m2g2(1-sinθ)2B2L2R
（3）金属棒达到最大速度的一半时，速度为v=mg(1-sinθ)B2L2
安培力为F安′=B2L2v2R
根据牛顿第二定律得：F-mgsinθ-F安′=ma
联立解得，a=F2m-12gsinθ
（4）根据能量守恒定律得：2QrQr+12mv2m+mg?4Lsinθ=F?4L
解得，QrQr=2FL-2mgLsinθ-2m3g2(1-sinθ)2B4L4
答：
（1）金属棒能达到的最大速度vm为2mg(1-sinθ)B2L2．
（2）灯泡的额定功率PL为m2g2(1-sinθ)2B2L2R．
（3）金属棒达到最大速度的一半时的加速度a为F2m-12gsinθ．
（4）金属棒由静止开始上滑4L的过程中，金属棒上产生的电热Qr为2FL-2mgLsinθ-2m3g2(1-sinθ)2B4L4．
本题解析：
本题难度：一般
5、计算题 （16分）光滑圆轨道和两倾斜直轨道组成如图所示装置，其中直轨道bc粗糙，直轨道cd光滑，两轨道相接处为一很小的圆弧。质量为m=0.1kg的滑块（可视为质点）在圆轨道上做圆周运动，到达轨道最高点a时的速度大小为v=4m/s，当滑块运动到圆轨道与直轨道bc的相切处b时，脱离圆轨道开始沿倾斜直轨道bc滑行，到达轨道cd上的d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计，已知圆轨道的半径为R=0.25m，直轨道bc的倾角θ=37o，其长度为L=26.25m，d点与水平地面间的高度差为h=0.2m，取重力加速度g=10m/s2，sin37°=0.6。求：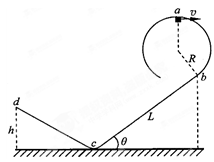
（1）滑块在圆轨道最高点a时对轨道的压力大小；
（2）滑块与直轨道bc问的动摩擦因数；
参考答案：（1）5.4N（2）0.8
本题解析：（1）在圆轨道最高点a处对滑块由牛顿第二定律得：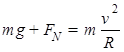
所以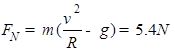
；
由牛顿第三定律得滑块在圆轨道最高点a时对轨道的压力大小为5.4N?
（2）从a点到d点全程由动能定理得：mg(R+Rcosθ+Lsinθ?h)?μmgcosθ?L＝0?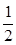
mv2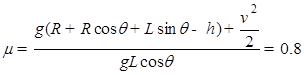
本题难度：一般