时间:2020-08-09 22:58:43
1、选择题 汽车两次通过同一凸形桥的最高点，第一次的速率比第二次大，则（ ）
A．第一次汽车对桥顶的压力较大
B．第二次汽车对桥顶的压力较大
C．第一次汽车所需向心力较大
D．第二次汽车所需向心力较大
参考答案：A、B以汽车为研究对象，设桥面对汽车的支持力大小为FN，由牛顿第二定律得，mg-FN=mv2r，得到FN=mg-mv2r，汽车对桥顶的压力大小FN′=FN=mg-mv2r，m、r一定，第一次的速率比第二次大，则第二次汽车对桥顶的压力较大．故A错误，B正确．
C、D由公式Fn=mv2r可知，m、r相同，第一次的速率比第二次大，第一次汽车所需向心力较大．故C正确，D错误．
故选BC
本题解析：
本题难度：简单
2、计算题 （12分）不可伸长的轻绳长l=1.2m，一端固定在O点，另一端系一质量为m=2kg的小球。开始时，将小球拉至绳与竖直方向夹角θ=37°的A处，无初速释放，如图所示，取sin37°=0.6,cos37°=0.8，g=10m/s2.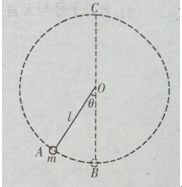
(1)求小球运动到最低点B时绳对球的拉力；
(2)若小球运动到B点时，对小球施加一沿速度方向的瞬时作用力F，让小球在竖直面内做完整的圆周运动，求F做功的最小值。
参考答案：（1）F=28N（2）W=55.2J
本题解析：第二问的分析应从小球能安全通过最高点的最小速度作为解题的突破口。（1）小球从A到B过程中，机械能守恒，有
mgl(1-cos37°)=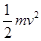
? ①
在B点，由牛顿第二定律有：
F-mg=m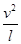
?②
联立①②解得：F=28N? ③
（2）设小球通过最高点的最小速度为vc，F做功的最小值为W
由牛顿第二定律：mg=m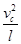
?④
从A到C的过程中由动能定理得
W-mgl(1+cos37°)=
-0? ⑤
联立④⑤解得：W=55.2J?⑥
评分标准：本题共12分，其中①②④每式2分，⑤式4分，③⑥每式1分
本题难度：一般
3、选择题 如图所示，长方体物块C置于水平地面上，物块A、B用不可伸长的轻质细绳通过滑轮连接（不计滑轮与 绳之间的摩擦），A物块与C物块光滑接触，整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动。下列说法正确的是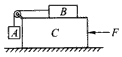
[? ]
A.B物块与C物块之间的接触面可能是光滑的
B.若推力f增大，则绳子对B物块的拉力必定增大
C.若推力F增大，则定滑轮所受压力必定增大
D.若推力F增大，则C物块对A物块的弹力必定增大
参考答案：AD
本题解析：
本题难度：一般
4、选择题 如图所示，物体甲的质量为2m，乙的质量为m，弹簧和悬线的质量可忽略不计。当悬线被烧断的瞬间，甲、乙的加速度数值为（?）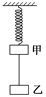
A．甲是0，乙是g
B．甲是g，乙是g
C．甲是0，乙是0
D．甲是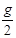
，乙是g
参考答案：D
本题解析：：细线烧断前，对甲乙整体受力分析，得出弹簧的弹力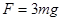
．细线烧断的瞬间，乙仅受重力，根据牛顿第二定律，有
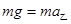，则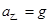
，方向竖直向下．对甲，弹簧的弹力在瞬间还未来得及改变，则有
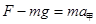，则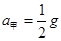
，方向竖直向上．
点评：解决本题的关键知道细线烧断的前后瞬间，弹簧的拉力由于来不及发生形变，弹力大小不变，然后根据牛顿第二定律求解．
本题难度：一般
5、选择题 如图所示，在倾角为θ的光滑斜劈P的斜面上有两个用轻质弹簧相连的物块A、B，C为一垂直固定在斜面上的挡板。A、B质量均为m，斜面连同挡板的质量为M，弹簧的劲度系数为k，系统静止于光滑水平面。现开始用一水平恒力F作用于P，（重力加速度为g）下列说法中正确的是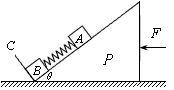
[? ]
A．若F=0，挡板受到B物块的压力为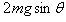
B．力F较小时A相对于斜面静止，F大于某一数值，A相对于斜面向上滑动
C．若要B离开挡板C，弹簧伸长量需达到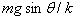
D．若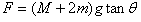
且保持两物块与斜劈共同运动，弹簧将保持原长
参考答案：AD
本题解析：
本题难度：一般