时间:2020-08-09 22:54:57
1、计算题 图中MN表示真空室中垂直于纸面的平板,它的一侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度大小为B。一带正电粒子从平板上狭缝O处以与平板成θ的初速度v射入磁场区域如图,最后到达平板上的P点。已知B、v以及P到O的距离l,不计重力,求此粒子的电荷量q与质量m之比。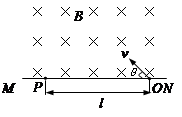
参考答案:
本题解析:带电粒子从O点垂直射入磁场,在洛伦兹力作用下做匀速圆周运动.又从P点射出磁场,则PO连线就是运动圆弧的直径,由长度、运动速度及磁场可确定粒子的比荷.
解:(1)由左手定则可知:粒子带正电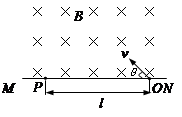
(2)粒子在磁场中做匀速圆周运动,设其半径为R ,
由几何关系可知:
由洛伦兹力公式和牛顿第二定律,有
qvB=m
由此得 
考点:带电粒子在匀强磁场中的运动.
点评:将带电粒子的入射点与出射点连线,即为圆弧对应的弦.当圆心落在弦上,则弦就是直径.
本题难度:一般
2、计算题 半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁感应强度为B,如图所示.一质量为m、带电荷量为q的正粒子(不计重力)以速度v从筒壁的A孔沿半径方向进入筒内,设粒子和筒壁的碰撞无电荷量和能量 的损失,那么要使粒子与筒壁连续碰撞
的损失,那么要使粒子与筒壁连续碰撞 ,绕筒壁一周后恰好又从A孔射出,问:?
,绕筒壁一周后恰好又从A孔射出,问:?
(1)磁感应强度B的大小必须满足什么条件?
(2)粒子在筒中运动的时间为多少?
参考答案: 解:(1)粒子射入圆筒后受洛伦兹力作用而偏转,设第一次与B点碰撞,碰后速度方向又指向O点,假设粒子与筒壁碰撞n-1次,运动轨迹是n段相等的圆弧,再从A孔射出.设第一段圆弧的圆心为O",半径为r(如图所示),则θ=2π/2n=π/n
解:(1)粒子射入圆筒后受洛伦兹力作用而偏转,设第一次与B点碰撞,碰后速度方向又指向O点,假设粒子与筒壁碰撞n-1次,运动轨迹是n段相等的圆弧,再从A孔射出.设第一段圆弧的圆心为O",半径为r(如图所示),则θ=2π/2n=π/n
由几何关系有:r=Rtan
又由r=
联立两式可以解得B= (n=3,4,5…)
(n=3,4,5…)
(2)每段圆弧的圆心角为
粒子由A到B所用时间
故粒子运动的总时间
本题解析:
本题难度:一般
3、计算题 利用如图所示装置可调控带电粒子的运动,通过改变左端粒子入射速度的大小,可以控制粒子到达右端接收屏上的位置,装置的上下两个相同的矩形区域内存在匀强磁场,磁感应强度大小均为B、方向与纸面垂直且相反,磁场区域的宽度均为h,磁场区域长均为15h,P、Q为接收屏上的二点,P位于轴线 上,Q位于下方磁场的下边界上。在纸面内,质量为m、电荷量为+q的粒子以某一速度从装置左端的中点射入,方向与轴线成370角,经过上方的磁场区域一次,恰好到达Q点。不计粒子的重力 (sin370=0.6、cos370=0.8)。问:
上,Q位于下方磁场的下边界上。在纸面内,质量为m、电荷量为+q的粒子以某一速度从装置左端的中点射入,方向与轴线成370角,经过上方的磁场区域一次,恰好到达Q点。不计粒子的重力 (sin370=0.6、cos370=0.8)。问:
(1)上下两磁场间距x为多少?
(2)仅改变入射粒子的速度大小,使粒子能打到屏上P点,求此情况下入射速度大小的所有可能值。
参考答案:(1)3h(2)
本题解析:(1)设粒子磁场中圆周运动半径为R
15h=3Rsin37°+
h=R(1-cos37°)
得x=3h
(2)一情况:设粒子经过上方磁场n次,下方磁场n次后到达P点,
由题意可知:15h=4n( +4nRNsin37°
+4nRNsin37°
解得:
讨论:又15-8n>0,即n<15/8 故 n=1, 
另一情况:经过上方磁场n次,下方磁场n-1次后到达P点
15h=(4n-2)( +(4n-2)RNsin37°
+(4n-2)RNsin37°
 由于粒子经过上方的磁场区域一次,恰好到达Q点,因此粒子不可能只经过上方一次射出后直接到达P点,因此有:n≥2 与19-8n>0得n=2。故只有一解:
由于粒子经过上方的磁场区域一次,恰好到达Q点,因此粒子不可能只经过上方一次射出后直接到达P点,因此有:n≥2 与19-8n>0得n=2。故只有一解:  不讨论,直接得结果不给分。
不讨论,直接得结果不给分。
考点:带电粒子在匀强磁场中的运动;动能定理.
本题难度:困难
4、计算题 (12分)如图所示,在以等边三角形abc为边界的区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B=1T,磁场方向垂直于abc平面向里。其中等边三角形边长L= m,P、Q分别是ac、bc的中点。一带正电的粒子(不计重力)从ab边中点O沿Oc方向以速度
m,P、Q分别是ac、bc的中点。一带正电的粒子(不计重力)从ab边中点O沿Oc方向以速度 射入,带电粒子恰好做匀速直线运动,从c点射出。
射入,带电粒子恰好做匀速直线运动,从c点射出。
(1)求电场强度的大小和方向;
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经过t=0.5s恰好从区域的边界中点Q射出。求粒子比荷q/m的大小;
(3)若仅撤去电场,带电粒子仍从O点同方向射入,且恰好也从区域的边界另一中点P射出,求粒子速度v的大小。
参考答案:(1)E=3N/C? E的方向a指向b
(2) ?C/kg
?C/kg
(3)v=4m/s
本题解析:(1)粒子由O至C匀速运动, ?
?
E=3N/C? E的方向a指向b
(2)仅撤去磁场后,带电粒子做类平抛运动,据题意由中点Q射出。
Oc方向上: t=0.5s?
Ob方向上: ?
?
 ?C/kg
?C/kg
(3)仅撤去电场,带电粒子在磁场中匀速圆周运动。据题意由中点P射出。
由几何关系: m
m
由 ?
?
代入得 v=4m/s
本题难度:一般
5、选择题 如图所示,在圆形区域内有方向垂直向里的匀强磁场.有一束速率各不相同的质子自A点沿半径方向射入磁场,这些质子在磁场中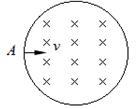
A.速度越大的,运动时间越长
B.运动时间越长的,其轨迹越长
C.速度越大的,速度的偏转角越小
D.所有质子在磁场中的运动时间相同
参考答案:C
本题解析:由于粒子相同,由周期公式 可知所有粒子的运动周期相同,速度越大,圆心角越小,运动时间较小,A错;同理BD错;速度越大的,圆心角越小,速度的偏转角越小,C对;
可知所有粒子的运动周期相同,速度越大,圆心角越小,运动时间较小,A错;同理BD错;速度越大的,圆心角越小,速度的偏转角越小,C对;
点评:难度中等,判断运动时间时,先看各个粒子的运动周期是否相同,在周期相同的情况下,运动时间与圆心角成正比
本题难度:一般