时间:2020-08-09 22:24:01
1、选择题 如图所示,质量为m、带电量为q的粒子以速度v0沿平行于两极板的方向射入偏转极板,最后打在荧光屏上.若两偏转极板电压为U,板间距为d,粒子打在灾光屏上的偏转距离为y,粒子从进入电场到打在屏上的时间为t,则下列说法正确的是(?)
A.若仅增大粒子的初速度v0,则t不变
B.若仅增大偏转电压U,则t变小
C.若仅减小粒子质量m,则y将变大
D.若仅减小两板间距离d,则y将不变
参考答案:C
本题解析:略
本题难度:一般
2、计算题 (10分)一束电子流在U1=500V的电压作用下得到一定速度后垂直于平行板间的匀强电场飞入两板间的中央,如图14所示.若平行板间的距离d=1cm,板长l=5cm,求:
(1)电子进入平行板间的速度多大?
(2)至少在平行板上加多大电压U2才能使电子不再飞出平行板?(电子电量1.6×10-19C,电子的质量9×10-31kg)
参考答案:(1)1.3×107m/s?(2)400V
本题解析:略
本题难度:简单
3、选择题 一带负电的粒子以某一初速度垂直于匀强电场方向飞入极板间.下列说法中正确的是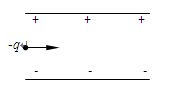
A.粒子向正极板偏转
B.电场力对粒子做负功
C.粒子在电场中做匀速直线运动
D.粒子在电场中运动的轨迹是圆弧
参考答案:A
本题解析:极板间的电场方向是竖直向下,由于粒子带负电,所以受到的电场力竖直向上,故粒子向正极板偏转,A正确;粒子在竖直方向上做初速度为零的匀加速直线运动,在竖直方向上的速度越来越大,所以电场对其做正功,B错误;由于粒子在电场中受力不平衡,做类平抛运动,C错误;粒子在电场中的轨迹为抛物线,D错误;
本题难度:简单
4、简答题 如图所示,长L="0." 4 m的两平行金属板A、B竖直放置,相距d="0." 02 m,两板间接入恒定电压为182 V且B板接正极一电子质量m="9." 1 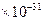 kg,电荷量
kg,电荷量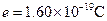 ,以
,以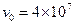 m/s的速度紧靠A板向上射入电场中,不计电子的重力.问电子能否射出电场?若能,计算在电场中的偏转距离;若不能,在保持电压不变的情况下,B板至少平移多少,电子才能射出电场?
m/s的速度紧靠A板向上射入电场中,不计电子的重力.问电子能否射出电场?若能,计算在电场中的偏转距离;若不能,在保持电压不变的情况下,B板至少平移多少,电子才能射出电场?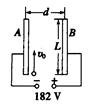
参考答案: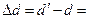 0.02m
0.02m
本题解析:设电子能射出极板,则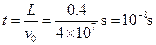
则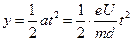
代入数值得:y="0.08" m>d,故不能射出.
若恰能射出,则B板需向右移动,板间距变为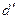
则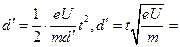 0.04m
0.04m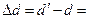 0.02m。
0.02m。
本题难度:一般
5、填空题 质量为m、电量为q的质点,在静电力作用下以恒定速率v沿圆弧从A点运动到B点,其速度方向改变的角度为θ(弧度),AB弧长为s。则A,B两点间的电势差ΦA-ΦB=_____,AB弧中点场强大小E=_____。
参考答案:0、mv2θ/qs
本题解析:由题意知电荷在静电力作用下做的是匀速圆周运动,从A点运动到B点,由动能定理知,静电力做的功是零,所以A、B两点间的电势差UAB=0(也可根据圆周是等势线判断);设场源电荷的电荷量为Q,质点做圆周运动的轨道半径为r,则弧长s=θr?①
静电力是质点做圆周运动的向心力,即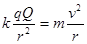 ?②
?②
弧AB中点的场强大小E=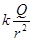 ?③
?③
解①②③组成的方程组得:E=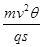
本题难度:简单