时间:2019-12-13 02:30:50
1、实验题 在验证力的平行四边形定则实验中,其中的三个实验步骤:
(1)在水平放置的木板上垫一张白纸,把橡皮条的一端固定在板上,另一端拴两根细线,通过细线同时用两个测力计互成角度地拉橡皮条,使它与细线的结点到达某一位置O点,在白纸上记下O点和两测力计的读数F1和F2.
(2)在纸上根据F1和F2的大小,应用平行四边形定则作图求出合力F′
(3)只用一只测力计通过细绳拉橡皮条,使它的伸长量与两测力计拉时相同,记下此时测力计的读数F.和细绳的方向.
以上三个步骤中均有错误或疏漏,请指出错在哪里?
(1)中是??
(2)中是??
(3)中是?
(4)、在实验中,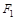 和
和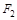 表示两个互成角度的力,
表示两个互成角度的力,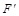 表示由平行四边形定则求出的合力,
表示由平行四边形定则求出的合力,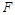 表示用一根弹簧测力计拉橡皮条的力,则下列图中符合实验事实的是
表示用一根弹簧测力计拉橡皮条的力,则下列图中符合实验事实的是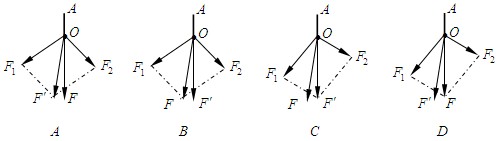
参考答案:(1)未记下细线的方向;(2)应根据F1和F2的大小和方向作图;(3)应将橡皮条与线的结点拉至原位置O点.(4) A
本题解析:该实验采用“等效法”进行,即一个弹簧秤和两个弹簧秤拉橡皮条与细绳套的结点时应该拉至同一位置O点,由于力是矢量,因此在记录数据时,不光要记录力的大小,还要记录其方向,这样才能做平行四边形,从而验证两个力的合力大小和方向是否与一个力的大小和方向相同.
F1与F2合力的实验值是指通过实验得到值,即用一个弹簧拉绳套时测得的力的大小和方向,F′方向应该与OA在一条直线上,即而理论值(实际值)是指通过平行四边形得出的值,故F是力F1与F2组成平行四边形的对角线,故A图比较符合题意
点评:明确实验目的和实验步骤是对实验的基本要求,同学们要在实际实验操作去理解实验目的和实验步骤,这样才能对实验有深刻的理解.
本题难度:一般
2、实验题 利用图示装置可以测定喷枪喷射油漆雾滴的速度。
将直径D = 40cm的纸带环,安放在一个可以匀速转动的转台上,纸带上有一狭缝A,A的正对面有一条标志线。油漆喷枪放在开有狭缝B的纸盒里。转台以角速度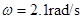 稳定转动后,开始喷漆,喷出来的雾滴运动速度认为不变。仅当狭缝A和B正对平行时,雾滴才能进入纸带环。改变喷射速度
稳定转动后,开始喷漆,喷出来的雾滴运动速度认为不变。仅当狭缝A和B正对平行时,雾滴才能进入纸带环。改变喷射速度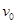 重复实验,已知
重复实验,已知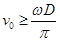 ,在纸带上留下了一系列的痕迹 a、b、c、d。将纸带取下放在刻度尺下,如图所示。
,在纸带上留下了一系列的痕迹 a、b、c、d。将纸带取下放在刻度尺下,如图所示。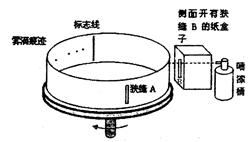

(1)速度最小的雾滴所留的痕迹应为?点,该点离标志线的距离为?cm。
(2)该喷枪喷出的雾滴的最大速度为?m/s,若考虑空气阻力的影响,该测量值
?真实值(选填“大于”“小于”或“等于”)。
参考答案:(1) a , 2.50; (2)24,小于;
本题解析:
试题分析:转盘的角速度一定,雾滴速度越大,运行时间越短,在雾滴运行的时间内,转盘转过的角度越小,故雾滴与标志线的距离越近;故a点对应雾滴的速度最小,毫米刻度尺读数要估读,为2.50cm。速度最大的是d点,距离标志线的距离是△s=0.70cm,根据t=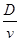 =
=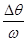 ,Δs=
,Δs=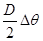 ,解得v=
,解得v=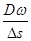 =24m/s;
=24m/s;
若考虑空气阻力,实际上雾滴做减速运动,现在将雾滴当做匀速直线运动的计算,求出来的速度要小于真实的速度。
本题难度:一般
3、简答题 一质量不计的弹簧原长为10cm,一端固定于质量m=2kg的物体上,另一端施一水平拉力F.(?g=10m/s2,设最大静摩擦力与滑动摩擦力相等)
(1)若物体与水平面间的动摩擦因数为0.2,当弹簧拉长至14cm时,物体恰好被拉动,弹簧的劲度系数多大?
(2)若将弹簧拉长至11cm时(物体在滑动过程中),物体所受的摩擦力大小为多少?
(3)物体静止时,若将弹簧拉长至13cm,物体所受到的摩擦力大小为多少?
参考答案:
(1)由题意得,物体与地面间最大静摩擦力
? fmax=μN=μmg=0.2×2×10N=4N
物体恰好被拉动,物体所受弹力等于最大静摩擦力:
? F1=kx1=fmax
得k=F1x1=fmaxx1=0.2×2×10(14-10)×10-2N/m=100N/m
(2)若将弹簧拉长至11cm时(物体在滑动过程中),物体相对地面滑动,受到滑动摩擦力为
? f2=μN=μmg=0.2×2×10N=4N
(3)弹簧弹力F3=kx3=100×(13-10)×10-2N=3N<fmax
物体受到静摩擦力,大小为f3=F3=3N.
答:(1)弹簧的劲度系数100N/m;
? (2)若将弹簧拉长至11cm时(物体在滑动过程中),物体所受的摩擦力大小为4N;
? (3)物体静止时,若将弹簧拉长至13cm,物体所受到的摩擦力大小为3N.
本题解析:
本题难度:一般
4、选择题 白云山风景区内有一种叫做“蹦极跳”的运动中,质量为m的游戏者身系一根长为L、弹性优良的轻质柔软的橡皮绳,从高处由静止开始下落1.5L时达到最低点,若不计空气阻力,则在弹性绳从原长达最低点的过程中的说法:①速度先减小后增大;②速度先增大后减小;③加速度先减小后增大;④加速度先增大后减小
以上说法正确的是( )
A.①③
B.②③
C.①④
D.②④
参考答案:B
本题解析:
本题难度:一般
5、选择题 如图所示的倾斜木板,在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ。现有10个质量均为m、半径均为r的均匀刚性球,在1号球的右侧有一光滑竖直挡板,若缓慢转动挡板至与斜面垂直,则在此过程中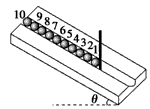
[? ]
A.1、2两球间的弹力不变
B.1球对挡板的压力逐渐减小
C.1球对斜面的压力逐渐增大
D.5、6两球间的弹力不变
参考答案:ABD
本题解析:
本题难度:一般