时间:2019-12-13 02:05:16
1、选择题 水平路面上转弯的汽车,向心力是( )
A.重力和支持力的合力
B.静摩擦力
C.重力、支持力、牵引力的合力
D.滑动摩擦力
参考答案:在水平路面上拐弯,向心力来源于静摩擦力,静摩擦力方向指向圆心.故B正确,ACD错误.
故选B.
本题解析:
本题难度:一般
2、选择题 如图所示,在双人花样滑冰运动中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,目测体重为G的女运动员做圆锥摆运动时和水平冰面的夹角约为30°,重力加速度为g,估算该女运动员
[? ]
A.受到的拉力为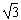 G
G
B.受到的拉力为2G
C.向心加速度为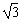 g
g
D.向心加速度为2g
参考答案:BC
本题解析:
本题难度:一般
3、简答题 (1)为了响应国家的“节能减排”号召,某同学采用了一个家用汽车的节能方法.在符合安全行驶的要求的情况下,通过减少汽车后备箱中放置的不常用物品和控制加油量等措施,使汽车负载减少.假设汽车以72km/h的速度行驶时,负载改变前、后汽车受到阻力分别为2000N和1950N.请计算该方法使发动机输出功率减少了多少?
(2)有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘.转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
参考答案:(1)v=72km/h=20m/s,由P=Fv得
?P1=F1v=f1v? ①
?P2=F2v=f2v? ?②
故△P=P1-P2=(f1-f2)v=1×103W,
(2)设转盘转动角速度为ω时,夹角为θ,
座椅到中心轴的距离:R=r+Lsinθ? ①
对座椅分析有:F心=mgtanθ=mRω2 ②
联立两式?得ω=
本题解析:
本题难度:一般
4、选择题 组成星球的物质是靠万有引力吸引在一起的,这样的星球有一个最大的自转速率。如果超过了该速率,星球的万有引力将不足以维持其赤道附近的物体做圆周运动。由此能得到半径为R、密度为ρ、质量为M且均匀分布的星球的最小自转周期T。下列表达式中正确的是
A.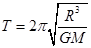
B.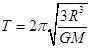
C.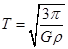
D.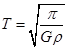
参考答案:AC
本题解析:由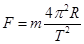 可得周期越小,物体需要的向心力越大,物体对星球表面的压力最小,当周期小到一定值时,压力为零,此时万有引力充当向心力,即
可得周期越小,物体需要的向心力越大,物体对星球表面的压力最小,当周期小到一定值时,压力为零,此时万有引力充当向心力,即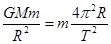 ,解得
,解得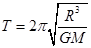 ,故A正确。因
,故A正确。因 ,代入上式可得:
,代入上式可得: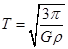 ,故C也正确。
,故C也正确。
本题难度:一般
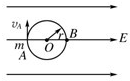
5、简答题 如图所示,一绝缘细圆环半径为r,其环面固定在竖直面上,场强为E的匀强电场与圆环平面平行,环上穿有一电荷量+q,质量为m的小球,可沿圆环做无摩擦的圆周运动,若小球经A点时速度vA的方向恰与电场垂直,且圆环与小球间沿水平方向无力的作用.
(1)求小环运动到A点的速度vA是多少?
(2)当小球运动到与A点对称的B点时,小球对圆环在水平方向上的作用力FB是多少?
(3)若E=
| mg q |
参考答案:(1)由题意可知小球到达A点时电场力提供向心力即qE=mv2Ar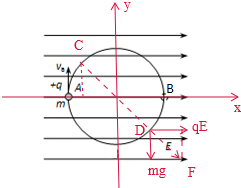
解得vA=
本题解析:
本题难度:一般