时间:2019-12-13 01:43:59
1、计算题 A、B为一平行板,板长为l,两板间距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里。一个质量为m,带电荷量为+q的带电粒子以一定初速度沿A、B两板中线且垂直于磁感线方向射入磁场中,粒子恰好从A板的右边界飞出。粒子重力不计。求:
(1)粒子在磁场中运动的轨道半径r和射入磁场的初速度v0各是多少?
(2)粒子在磁场中运动的时间t是多少? 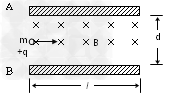
参考答案:解:(1)设粒子做圆周运动的圆心为O(如图)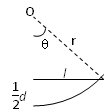
由几何条件可知:r2=l2+(r-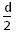 )2?①
)2?①
解之得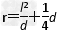
由牛顿第二定律可得:qv0B=m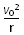 ?②
?②
解①、②式得v0=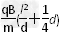
(2)设粒子从磁场飞出时,转过的圆心角为θ,粒子做圆周运动的周期为T,则有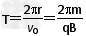 ?③
?③
tgθ=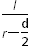 ?④
?④
t=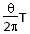 ?⑤
?⑤
解①、③、④、⑤得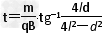 或
或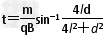
本题解析:
本题难度:一般
2、计算题 如图所示,有三个宽度均相等的区域I、Ⅱ、Ⅲ;在区域I和Ⅲ内分别为方向垂直于纸面向外和向里的匀强磁场(虚线为磁场边界面,并不表示障碍物),区域I磁感应强度大小为B,某种带正电的粒子,从孔O1以大小不同的速度沿图示与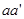 夹角α=300的方向进入磁场(不计重力)。已知速度为v0和2v0时,粒子仅在区域I内运动且运动时间相同,均为t0。
夹角α=300的方向进入磁场(不计重力)。已知速度为v0和2v0时,粒子仅在区域I内运动且运动时间相同,均为t0。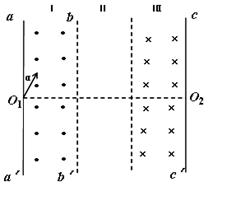
(1)试求出粒子的比荷q/m、速度为2v0的粒子从区域I射出时的位置离O1的距离L;
(2)若速度为v的粒子在区域I内的运时间为t0/5,在图中区域Ⅱ中O1O2上方加竖直向下的匀强电场,O1O2 下方对称加竖直向上的匀强电场,场强大小相等,使速度为v的粒子每次均垂直穿过I、Ⅱ、Ⅲ区域的边界面并能回到O1点,则请求出所加电场场强大小与区域Ⅲ磁感应强度大小。
参考答案:(1)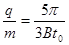 ;
;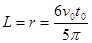 (2)
(2)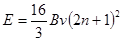 ;
;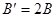
本题解析:(1)由题意可得速度为v0和2v0的粒子均由区域I左侧aa´出磁场 (1分)
则粒子转过的圆心角为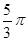 (1分)
(1分)
故 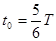 (1分)
(1分)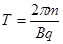 (1分)
(1分)
解得: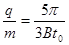 (2分)
(2分)
对速度为2v0的粒子在区域I运动: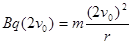 (2分)
(2分)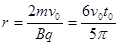 (1分)
(1分)
由几何关系可得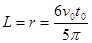 (2分)
(2分)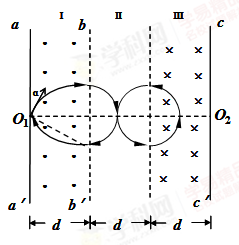
(2)当速度为v时,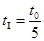 , 圆心角
, 圆心角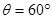 (1分)
(1分)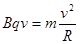
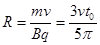 (1分)
(1分)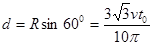 (1分)
(1分)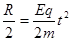 (1分)
(1分)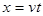 (1分)
(1分)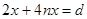 (n=0、1、2、3…… ) (1分)
(n=0、1、2、3…… ) (1分)
得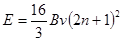 (2分)
(2分)
在区域中:带电粒子做圆周运动的半径为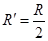 (1分)
(1分)
即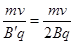 所以:
所以: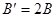 (2分)
(2分)
考点:本题考查带电粒子在匀强磁场中的运动
本题难度:困难
3、简答题 如图,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于x?y平面向外.P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点.A是一块平行于x轴的挡板,与x轴的距离为
| h 2 |
| a 2 |

参考答案: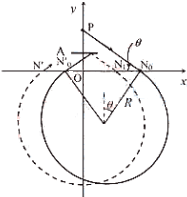
设粒子的入射速度为v,第一次射出磁场的点为N′0,与板碰撞后再次进入磁场的位置为N1,子在磁场中运动的轨道半径为R,有R=mvqB…(1)
粒子速率不变,每次进入磁场与射出磁场位置间距离x1保持不变有x1=N0′N0=2Rsinθ…(2)
粒子射出磁场与下一次进入磁场位置间的距离x2始终不变,与N0′N0相等.由图可以看出x2=a…(3)
设粒子最终离开磁场时,与档板相碰n次(n=0、1、2、3…).
若粒子能回到P点,由对称性,出射点的x坐标应为-a,即(n+1)x1-nx2=2a…(4)
由(3)(4)两式得x1=n+2n+1a…(5)
若粒子与挡板发生碰撞,有x1-x2>a4…(6)
联立(3)(4)(6)得:n<3…(7)
联立(1)(2)(5)得:v=qB2msinθ?n+2n+1a…(8)
把sinθ=h
本题解析:
本题难度:一般
4、选择题 等腰直角三角形ABC区域内(含边界)有垂直纸面向里的匀强磁场,磁感应强度为B,t=0时刻有一束质量均为m、电荷量均为q的正离子由直角顶点B沿BC方向射入磁场,可认为所有离子都是同时进入磁场且各离子速度大小不等,不计离子的重力及离子间的相互作用,则( )
A.同一时刻,磁场中的所有离子都在同一直线上
B.由AB边界射出的离子在磁场中运动的时间均为
| πm qB |
| πm 4qB |
| 3πm 4qB |
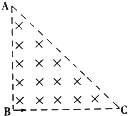
参考答案:粒子在磁场中做匀速圆周运动,匀速圆周运动的周期:T=2πmqB,轨道半径r=mvqB;
A、同一时刻即经历相同的时间,则转过的圆心角相同,如下图中的E、E、F三点,因为O1、O2、O3三点共线,由几何知识知DEF三点共线,即任何同一时刻磁场中的所有离子都在同一直线上,故A正确;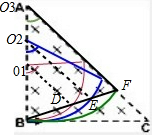
B、由AB边界射出的离子运动轨迹如下图所示,其运动的轨迹均为半圆,则转过的圆心角均为π2,运动时间均为:T2=πmqB,故B正确;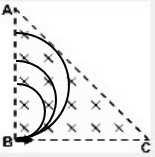
C、由AC边界射出的离子在磁场中运动的轨迹如下图所示,当粒子运动轨迹与AC相切时,粒子恰好不能从AC边射出,此时粒子转过的圆心角为135°,粒子的运动时间t=135°360°×2πmqB=3πm4qB,当粒子转过的圆心角大于135°粒子不能从AC边射出,故C错误,D正确;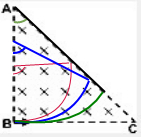
故选:ABD.
本题解析:
本题难度:简单
5、简答题 如图所示,一束电子(电量为e)以速度v0垂直射入磁感应强度为B,宽为d的匀强磁场中,电子穿出磁场的速度方向与电子原来的入射方向的夹角为30°,(电子重力忽略不计)
求:
(1)电子的质量是多少?
(2)穿过磁场的时间是多少?
(3)若改变初速度大小,使电子刚好不能从A边射出,则此时速度v是多少?
参考答案:(1)电子在磁场中运动,只受洛伦兹力作用,故其轨迹是圆弧的一部分,又因为F洛⊥v,故圆心在电子穿入和穿出磁场时受到洛伦兹力指向的交点上,设圆心为O点.如图所示.
由几何知识可知,圆心角θ=30°,OC为半径r,则得
r=dsin30°=2d
又由r=mveB得
得m=2dBev0
(2)电子穿过磁场的时间是t=30°360°T=112T
由于T=2πmeB,故t=2πm12Be=πd3v0
(3)电子刚好不能从A边射出时,轨迹恰好与磁场右边界相切,由几何知识得R=2d,
由R=mveB=2d
得v=12v0.
答:
(1)电子的质量是2dBev0.
(2)穿过磁场的时间是πd3v0.
(3)若改变初速度大小,使电子刚好不能从A边射出,则此时速度v是12v0.
本题解析:
本题难度:一般