时间:2019-12-13 01:27:13
1、选择题 B组:空间存在一匀强磁场B,其方向垂直纸面向里,另有一个点电荷+Q的电场,如图所示,一带电-q的粒子以初速度v0从某处垂直电场、磁场入射,初位置到点电荷的距离为r,则粒子在电磁场中的运动轨迹可能为( )
A.以点电荷+Q为圆心,以r为半径的在纸平面内的圆周
B.开始阶段在纸面内向向右偏转的曲线
C.开始阶段在纸面内向向左偏转的曲线
D.沿初速度v0方向的直线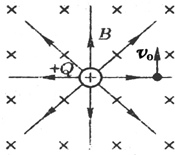
2、简答题 如图所示,BC为半径R=0.144m的
| 1 4 |
| mP mQ |
3、选择题 如图所示,细杆的一端与一小球相连,可绕过O的水平轴自由转动.现给小球一初速度,使它做圆周运动.图中a、b分别表示小球轨道的最低点和最高点,则杆对球作用力可能是( )
A.a处为拉力,b处为拉力
B.a处为推力,b处为拉力
C.a处为拉力,b处为推力
D.a处为推力,b处为推力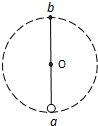
4、选择题 如图所示的两轮靠皮带传动,皮带没有打滑,A、B、C三点的位置关系如图,若r1>r2,O1C=r2,则三点的向心加速度的关系为
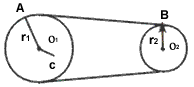
[? ]
5、选择题 一根长为L的轻杆下端固定一个质量为m的小球,上端连在光滑水平轴上,轻杆可绕水平轴在竖直平面内运动(不计空气阻力).当小球在最低点时给它一个水平初速度v0,小球刚好能做完整的圆周运动.若小球在最低点的初速度从v0逐渐增大,则下列判断正确的是
[? ]
A.小球能做完整的圆周运动,经过最高点的最小速度为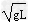
B.小球在最高点对轻杆的作用力先减小后增大
C.小球在最低点对轻杆的作用力先减小后增大
D.小球在运动过程中所受合外力的方向始?终指向圆心