高考物理知识点《牛顿第二定律及应用》考点强化练习（2019年练习版） - 高考物理题库

1、填空题如右图所示，质量之比2:1的球A、B，由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀速运动的电梯内，细线承受的拉力为F；某时刻突然剪断细线，那么在细线断的瞬间，弹簧的弹力大小为___________；小球A的加速度大小为_________

参考答案：0.33F?，? 1.5g

本题解析：由于弹簧形变量较大，在间断细线的瞬间弹簧弹力不能发生突变，在匀速运动阶段F=3mg，kx=2mg，kx=0.33F，小球A受到竖直向下的重力2mg和竖直向下的弹簧弹力mg的作用，所以加速度为1.5g
点评：难度较小，明确模型的类型，如果是细绳，则弹力可以突变，如果是弹簧或橡皮筋则弹力不能突变

本题难度：简单

2、计算题 “翻滚过山车”的物理原理可以用如图所示装置演示，光滑斜槽轨道AD与半径为R＝0.1m的竖直圆轨道(圆心为O)相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB＝37°.质量为m＝0.1kg的小球从距D点L＝1.3m处由静止开始下滑，然后冲上光滑的圆形轨道(g＝10m/s2，sin37°＝0.6，cos37°＝0.8)．求：
(1)小球在光滑斜槽轨道上运动的加速度的大小；
(2)小球通过B点时对轨道的压力的大小；
(3)试分析小球能否通过竖直圆轨道的最高点C，并说明理由．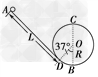

参考答案：解：(1)在光滑斜槽上由牛顿第二定律得：
mgsin37°＝ma.
故a＝gsin37°＝6m/s2
(2)小球由A至B，机械能守恒，
则mg(Lsin37°＋hDB)＝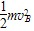
hDB＝R(1－cos37°)
又小球在B点，由牛顿第二定律得：
FNB＝mg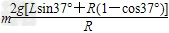＋＝17N
由牛顿第三定律得：小球过B点时对轨道的压力大小为17N.
(3)小球要过最高点，需要的最小速度为v0
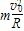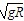则mg＝即v0＝＝1m/s
又小球从A到C机械能守恒，
所以mg[Lsin37°－R(1＋cos37°)]＝mv
解之vC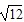＝m/s>1m/s
故小球能过最高点C.

本题解析：

本题难度：一般

3、计算题将金属块m用压缩的轻弹簧卡在一个矩形的箱中，如图所示，在箱的上顶板和下底板装有压力传感器，箱可以沿竖直轨道运动，金属块始终没有离开上顶板。当箱以a="2.0" m/s2的加速度竖直向上做匀减速运动时，上顶板的压力显示压力为6.0 N，下底板的压力传感器显示的压力为10.0 N。（g="10" m/s2）

（1）金属块的重力多大?
（2）若上顶板压力传感器的示数是下底板压力传感器的示数的0.4倍，试求箱的加速度大小和方向。
（3）要使上顶板压力传感器的示数为零，箱沿竖直方向运动的情况可能是怎样的?

参考答案：（1）5N?（2）a=1m/s2，竖直向上?（3）以a=10m/s2的加速度向上加速或向下减速

本题解析：（1）以物体为研究对象，物体受重力、弹簧支持力、上顶板的压力，根据牛顿第二定律，，所以，金属块的重力为5N
（2）只要上顶板有压力，说明弹簧的形变量不变，即下底板压力不变为10N，则上顶板压力为4N，根据牛顿第二定律可知，，则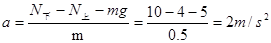，方向竖直向上
（3）若上顶板压力传感器的示数为零，则对物体有：，可得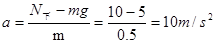，方向竖直向上，所以物体可能以a=10m/s2的加速度向上加速或向下减速

本题难度：一般

4、选择题如右图所示两段长均为L的轻质线共同系住一个质量为m的小球，另一端分别固定在等高的A、B两点，A、B两点间距也为L，今使小球在竖直平面内做圆周运动，当小球到达最高点时速率为v，两段线中张力恰好均为零，若小球到达最高点时速率为2v，则此时每段线中张力大小为(　)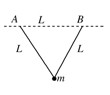

A. 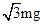? B．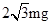
C．3mg? D．4mg

参考答案：A

本题解析：当小球到达最高点速率为v时，有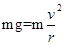当小球到达最高点速率为2v时，应有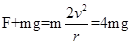，所以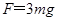，此时最高点各力如图所示，所以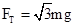，A正确．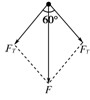

点评：本题是竖直平面内圆周运动问题，关键是分析物体受力，确定向心力的来源．基本题，比较容易．

本题难度：一般

5、计算题（16分）素有“陆地冲浪”之称的滑板运动已深受广大青少年喜爱．如图所示是由足够长的斜直轨道,半径的凹形圆弧轨道和半径的凸形圆弧轨道三部分组成的模拟滑板组合轨道.这三部分轨道依次平滑连接,且处于同一竖直平面内．其中M点为凹形圆弧轨道的最低点,N点为凸形圆弧轨道的最高点，凸形圆弧轨道的圆心O与M点在同一水平面上.可视为质点,质量为的滑板从斜直轨道上的P点无初速度滑下,经M点滑向N点,P点距水平面的高度.不计一切阻力,取.求：

(1)滑板滑至M点时的速度；
(2)滑板滑至M点时，轨道对滑板的支持力；
(3)若滑板滑至N点时恰好对轨道无压力，则滑板的下滑点P距水平面的高度应变为多少.