时间:2019-07-11 04:11:34
1、选择题 如图所示,闭合导线框的质量可以忽略不计,将它从图示位置匀速拉出匀强磁场,若第一次用0.3s时间拉出,外力做的功为 ,通过导线截面的电量为
,通过导线截面的电量为 ,第二次用0.9s时间拉出,外力做的功为
,第二次用0.9s时间拉出,外力做的功为 ,通过导线截面的电量为
,通过导线截面的电量为 ,则(?)
,则(?)
A. ,
,
B. ,
,
C. ,
,
D. ,
,
2、选择题 穿过一个电阻为2Ω的闭合线圈的磁通量每秒均匀减小0.4Wb,则线圈中
[? ]
A、感应电动势为0.4V
B、感应电动势每秒减小0.4V
C、感应电流恒为0.2A
D、感应电流每秒减小0.2A
3、计算题 一个电阻为r、边长为L的正方形线圈abcd共N匝,线圈在磁感应强度为B的匀强磁场中绕垂直于磁感线的轴OO"以如图所示的角速度ω匀速转动,外电路电阻为R。
(1)在图中标出此刻线圈中感应电流的方向。
(2)转动过程中感应电动势的峰值有多大?
(3)线圈平面与磁感线夹角为60°时的感应电动势多大?
(4)从图示位置开始,线圈转过60°的过程中通过R的电荷量是多少? 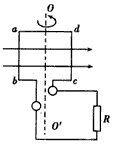
4、选择题 如图所示,有一矩形线圈,面积为S,匝数为N,整个线圈的电阻为r,在磁感应强度为B的磁场中,绕OO′轴以角速度ω匀速转动,外电阻为R,当线圈由图示位置转过90°的过程中,下列说法正确的是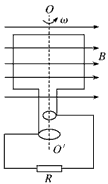
[? ]
A.磁通量的变化量为ΔΦ=NBS
B.平均感应电动势为E=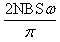
C.电阻R所产生的焦耳热为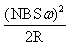
D.通过电阻R的电荷量为q=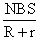
5、选择题 穿过闭合回路的磁通量Φ随时间t变化的图像分别如图甲、乙、丙、丁所示,下列关于回路中产生的感应电动势的论述,正确的是
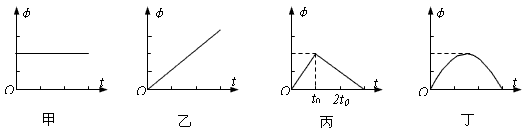
[? ]