时间:2019-07-11 04:10:24
1、选择题 在水平绝缘地面上放置着质量为m．带电量为+q的物块，在竖直方向上加一个向上的电场，场强E随时间t的变化规律如图所示，不考虑运动过程中受到的空气阻力，重力加速度为g，从t=0开始释放带电物块，在0～4t0时间内（ ）
A．在t0时刻物块动能最大
B．在2t0时刻物块的重力势能最大
C．在3t0时刻物块的电势能最大
D．在3t0时刻物块的机械能最大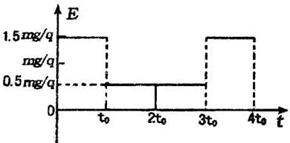
参考答案：A、根据分析可知，物块的运动情况：在0～t0时间内，向上做匀加速运动；在t0～2t0时间内，向上做匀减速运动；在2t0～3t0时间内，向下做匀加速运动；在3t0～4t0时间内，向下做匀减速运动；可见，t0时刻物块的速度最大，其动能最大．故A正确．
? B、在2t0时刻物块离地面高度最大，其重力势能最大．故B正确．
? C、当物块向上运动时，电场力做正功，电势能减小，则物块在0时刻和4t0时刻电势能最大．故C错误．
? D、根据能量守恒可知，物块的电势能与机械能的总量不变，在2t0时刻物块的电势能最小，其机械能最大．故D错误．
故选AB
本题解析：
本题难度：一般
2、选择题 质量为m的物体，在距地面h高处以g/2的加速度由静止开始竖直落下至地面，则下落过程中（ ）
A．物体的动能增加3mgh/2
B．物体的重力势能减少了mgh/2
C．物体的机械能减少了mgh
D．物体的重力做的功为mgh
参考答案：D
本题解析：据题意，重力做功mgh，其他力做功mgh/2，则据动能定理，物体动能增加了mgh/2，故选项A错误而选项D正确；物体重力势能减少量等于重力做的功，即mgh，故选项B错误；物体机械能减少量等于其他力做的功，即mgh/2，故选项C错误。
考点：本题考查动能定理。
本题难度：一般
3、填空题 如图两截半径分别为2R和R的圆筒，底部放在同一水平面上，大筒内装的高度为H、密度为ρ的液体，现把连接两筒的阀门打开，使两筒中液体高度相等，则这一过程中重力做功为______．（连接处液体可忽略）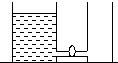
参考答案：两截半径分别为2R和R的圆筒，底部放在同一水平面上，大筒内装的高度为H、密度为ρ的液体，
现把连接两筒的阀门打开，使两筒中液体高度相等，此时液体的高度为h，
所以π（2R）2H=πR2h+π（2R）2h
h=45H
所以从大筒移到小筒的液体体积为V=45πR2H
所以这个过程液体的重力势能变化量等于大筒上部分的液体移到右则小筒里的重力势能变化．
即mgh′=45ρπR2Hg?H2=25πρgH2R2
故答案为：25πρgH2R2
本题解析：
本题难度：一般
4、选择题 如图所示，质量为m的跳高运动员先后用背越式和跨越式两种跳高方式跳过某一高度，该高度比他起跳时的重心高出h，则他从起跳后至越过横杆的过程中克服重力所做的功下面答案错误的是（ ）
A．都必须大于mgh
B．都不一定大于mgh
C．用背越式不一定大于mgh，用跨越式必须大于mgh
D．用背越式必须大于mgh，用跨越式不一定大于mgh
参考答案：从起跳后至越过横杆的过程中，跨越式跳高时运动员克服重力所做的功一定大于mgh，而背越式跳高时不一定大于mgh，也可以小于mgh，也可以等于mgh．故ABD错误，C正确．
本题选错误的，故选ABD．
本题解析：
本题难度：一般
5、计算题 （18分）如图所示，固定在地面上的光滑圆弧面底端与车C的上表面平滑相接，在圆弧面上有一滑块A，其质量mA=2kg，在距车的水平面高h=1.25m处由静止下滑，车C的质量为mC=6kg．在车C的左端有一质量mB=2kg的滑块B，滑块B与A均可视作质点，滑块A与B碰撞后立即粘合在一起共同运动，最终没有从车C上滑落．已知滑块A、B与车C的动摩擦因数均为μ=0.5，车C与水平面间的摩擦忽略不计，取g=10m/s2．求：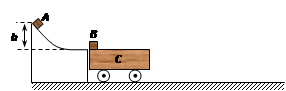
（1）滑块A滑到圆弧面底端时的速度大小；
（2）滑块A与B碰撞后瞬间的共同速度大小；
（3）车C的最短长度．
参考答案：（1）5(m/s)（2）2.5(m/s)（3）L="0.375(m)"
本题解析：（1）设滑块A滑到圆弧末端时的速度大小为v1，由机械能守恒定律有：
mAgh=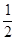
mAv12? ①（3分）
代入数据，由①式解得：v1="5(m/s)" （2分）
（2）设A、B碰撞后瞬间的共同速度为v2，滑块A与B组成的系统动量守恒，由动量守恒定律可得：
mAv1=(mA+mB)v2? ②（3分）
代入数据，由②式解得：v2="2.5(m/s)" （2分）
（3）设车C的最短长度为L，滑块A与B最终没有从车C上滑出，三者的最终速度相同，设其共同速度为v3，根据动量守恒和能量守恒定律可得：
(mA+mB)v2 =(mA+mB+mC)v3 ③（3分）
μ(mA+mB)gL=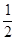(mA+mB)v22-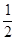(mA+mB+mC)v32? ④（3分）
联立③④式可解得：L="0.375(m)" （2分）
本题考查机械能守恒和动量守恒定律的应用，A由最高点滑到最低点过程中只有重力做功，机械能守恒，A、B碰撞瞬间，小车不参与碰撞，以A、B为系统动量守恒，求得碰后速度，AB结合为一个整体，当与C相对静止时系统速度相同，且减小的动能完全用于克服摩擦力做功，由能量守恒定律可求解
本题难度：一般