时间:2019-07-11 03:29:21
1、选择题 在光滑的水平桌面上，有甲、乙两木块，两木块之间夹一轻质弹簧，弹簧仅与木块接触但不连接，用两手拿住两木块压缩弹簧，并使两木块静止，则（ ）
A．两手同时释放弹簧，两木块的总动量为零
B．甲木块先释放，乙木块后释放，两木块的总动量指向甲木块一方
C．甲木块先释放，乙木块后释放，两木块的总动量指向乙木块一方
D．甲木块释放后至乙木块释放前的这一过程中，两木块的总动量守恒
2、选择题 关于弹簧测力计上零刻度的意义，下列说法中错误的是
A．弹簧的长度为零
B．弹簧的伸长为零
C．弹簧所受的拉力为零
D．指针的初始位置
3、选择题 如图所示，自由落下的小球，从接触竖直放置的弹簧开始到弹簧的压缩量最大的过程中，对于小球的受力和运动，下列说法中正确的是（ ）
A．弹簧弹力一直在增大，合力先变小后变大
B．合力先变大后变小，速度先变小后变大
C．速度最大时，弹簧弹力也最大
D．弹簧弹力的最大值大于2倍的小球重力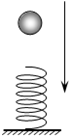
4、选择题 如图所示，自由落下的小球，从接触竖直放置的弹簧开始到弹簧的压缩量最大的过程中，下列说法正确的是（ ）
A．小球所受重力不变
B．小球所受弹力改变
C．小球的加速度不变
D．小球的速度改变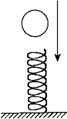
5、实验题 (6分)学校科技活动小组的同学们准备自己动手粗略测定铁块与长木板之间的动摩擦因数，已有的器材：长木板、小铁块、米尺和刻度尺.他们同时从实验室借来一个电火花打点计时器，设计了如下实验：
a.用米尺测量长木板总长度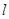
，将打点计时器固定在长木板上。然后将长木板靠在竖直墙壁固定（如图），并测量长木板顶端B相对于水平地面的高度
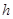和长木板底端A与墙角C之间的距离
；
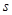b.将小铁块连上纸带，接通打点计时器后释放，得到的纸带如下图, A、B、C、D、E是纸带上连续的5个点。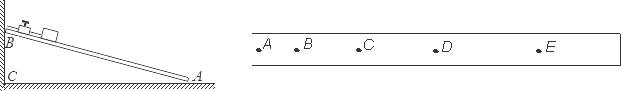
现用刻度尺直接测出AC、CE的距离分别为：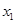
、
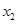；已知交流电的频率为
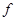，重力加速度为
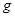.由此可求得铁块的加速度
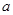＝?；根据牛顿第二定律，可求得动摩擦因数
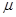＝?(用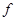、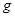和测得物理量的字母表示) 。?