时间:2019-07-11 03:14:21
1、简答题 某同学做拍打篮球的游戏，要控制篮球，使其重心在距地面高度为h=0.9m的范围内做竖直方向上的往复运动，如图所示．每次要在最高点时用手开始击打篮球，手与球作用一段距离后分开，球落地反弹．已知球反弹的速度v2的大小是落地速度v1大小的4/5，反弹后恰好达到最高点，球与地面的作用时间为t=0.1s，篮球的质量m=0.5kg，半径为R=0.1m，若地面对球的作用力可视为恒力，篮球与地面碰撞时认为重心不变，忽略空气阻力和篮球的转动．求
（1）球反弹的速度v2．
（2）地面对球的作用力F（g取10m/s2）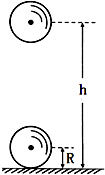
参考答案：（1）从球反弹后至达最高点，此过程由0-v22=-2g（h1-R），
可得：v2=
本题解析：
本题难度：一般
2、填空题 一个质量是0.2kg的钢球，以2m/s的速度水平向右运动，碰到一块竖硬的大理石后被弹回，沿着同一直线以2m/s的速度水平向左运动，碰撞前后钢球的动量的改变量大小为______，kgm/s，若时间为0.2S，钢球碰撞碰撞过程受到平均作用力大小为______N．
参考答案：设水平向右为正，
△P=P2-P1=mv2-mv1=0.2×（-2-2）kgm/s=-0.8kgm/s，所以大小为0.8kgm/s．
根据动量定理得：
Ft=△P
解得：F=△Pt=0.80.2N=4N
故答案为：0.8；4
本题解析：
本题难度：一般
3、计算题 对于同一物理问题，常常可以从宏观与微观两个不同角度进行研究，找出其内在联系，从而更加深刻地理解其物理本质。
（1）一段横截面积为S、长为l的直导线，单位体积内有n个自由电子，电子电荷量为e。该导线通有电流时，假设自由电子定向移动的速率均为v。
（a）求导线中的电流I；
（b）将该导线放在匀强磁场中，电流方向垂直于磁感应强度B，导线所受安培力大小为F安，导线内自由电子所受洛伦兹力大小的总和为F，推导F安=F。
（2）正方体密闭容器中有大量运动粒子，每个粒子质量为m，单位体积内粒子数量n为恒量。为简化问题，我们假定：粒子大小可以忽略；其速率均为v，且与器壁各面碰撞的机会均等；与器壁碰撞前后瞬间，粒子速度方向都与器壁垂直，且速率不变。利用所学力学知识，导出器壁单位面积所受粒子压力F与m、n和v的关系。
（注意：解题过程中需要用到、但题目没有给出的物理量，要在解题时做必要的说明）
参考答案：（1）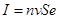
?证明见答案?（2）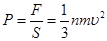
本题解析：（1）（a）电流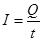
，又因为
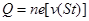，代入则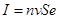
（b）F安=BIL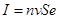，，代入则：F安=BnvSeL；因为总的自由电子个数N=nSL，每个自由电子受到洛伦兹力大小f=Bve，所以F=Nf=BnvSeL=F安，即F安=F。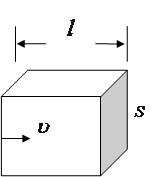
（2）气体压强公式的推导：设分子质量为m，平均速率为v，单位体积的分子数为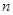
；建立图示柱体模型，设柱体底面积为
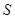，长为
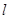，则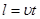
柱体体积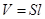 
柱体内分子总数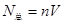 
因分子向各个方向运动的几率相等，所以在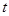
时间内与柱体底面碰撞的分子总数为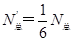
设碰前速度方向垂直柱体底面且碰撞是弹性的，则分子碰撞器壁前后，总动量的变化量为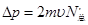
依据动量定理有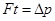 
又压力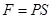 
由以上各式得单位面积上的压力?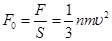
【点评】本题的第1题中两问都曾出现在课本中，例如分别出现在人教版选修3-1.P42，选修3-1P.42，这两个在上新课时如果老师注意到，并带着学生思考推导，那么这题得分是很容易的。第2问需要利用动量守恒知识，并结合热力学统计知识，通过建立模型，然后进行推导，这对学生能力要求较高，为了处理相应问题，通过建模来处理问题。在整个推导过程并不复杂，但对分析容易对结果造成影响的错误是误认为所有分析都朝同一方向运动，而不是热力学统计结果分子向各个运动方向运动概率大致相等，即要取总分子个数的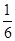
。
【考点定位】电流微观表达式、洛伦兹力推导以及压强的微观推导。
本题难度：一般
4、计算题 如图所示，长为L的木板A静止在光滑的水平桌面上，A的左端上方放有小物体B（可视为质点），一端连在B上的细绳，绕过固定在桌子边沿的定滑轮后，另一端连在小物体C上，设法用外力使A、B静止，此时C被悬挂着。A的右端距离滑轮足够远，C距离地面足够高。已知A的质量为6m，B的质量为3m，C的质量为m。现将C物体竖直向上提高距离2L，同时撤去固定A、B的外力。再将C无初速释放，当细绳被拉直时B、C速度的大小立即变成相等，由于细绳被拉直的时间极短，此过程中重力和摩擦力的作用可以忽略不计，细绳不可伸长，且能承受足够大的拉力。最后发现B在A上相对A滑行的最大距离为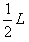
。细绳始终在滑轮上，不计滑轮与细绳之间的摩擦，计算中可认为A、B之间的最大静摩擦力等于滑动摩擦力，取重力加速度g=10m/s2。
（1）求细绳被拉直前瞬间C物体速度的大小υ0；
（2）求细绳被拉直后瞬间B、C速度的大小υ；
（3）在题目所述情景中，只改变C物体的质量，可以使B从A上滑下来。设C的质量为km，求k至少为多大？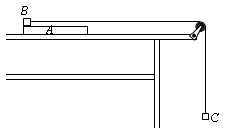 
参考答案：解：（1）C做自由落体运动，下降高度为2L时的速度为v0，根据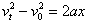
得
v0=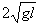
（2）此时细绳被拉直，B、C速度的大小立即变成v，设绳子对B、C的冲量大小为I，根据动量定理得
对B：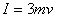
对C：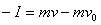
解得B、C速度的大小v=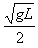
（3）设C物体的质量为km，A、B之间的动摩擦因数为μ
由（2）可知，细绳被拉直时B、C速度的大小v′′=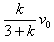
此后B物体的加速度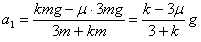
A物体的加速度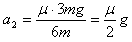
经时间t，B物体的速度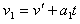
，B物体的位移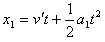
同样，A物体的速度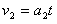
，A物体的位移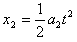
（i）根据题意，若k=1，当v1=v2时，x1－x2=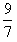
，解μ=0.4
（ii）要使v1=v2时，x1－x2=L，利用（i）求得的动摩擦因数μ，可得k=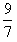=1.29
即C物体的质量至少为1.29m时，才可以使B物体从A上滑下来
本题解析：
本题难度：困难
5、选择题 古时有“守株待兔”的寓言.设兔子的头部受到大小等于自身体重的打击力时即可致死，并设兔子与树桩作用时间为0.2 s，则被撞死的兔子其奔跑速度可能为（取g="10" m/s2）（?）
A．1 m/s
B．1.5 m/s
C．2 m/s
D．2.5 m/s
参考答案：C
本题解析：根据动量定理：-Ft=-mv及F=mg求解得v="2" m/s.
本题难度：简单