时间:2019-07-03 00:19:37
1、选择题 如图表示撑杆跳运动的三个阶段:助跑、撑杆起跳、越横杆,其中发生了弹性势能与重力势能转化的阶段是( )
A.只有助跑阶段
B.只有撑杆起跳阶段
C.只有越横杆阶段
D.撑杆起跳阶段与越横杆阶段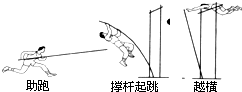
2、简答题 如图7所示,一个光滑的弧形槽AB与水平粗糙轨道BC面相连接,另一圆形光滑轨道竖直放置与BC相切于C点,小球在离地面高h=0.45m的A点沿弧形槽静止开始滑下,进入水平轨道BC后,再进入圆形轨道内。已知小球在BC段动摩擦因数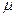 =0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求:
=0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求: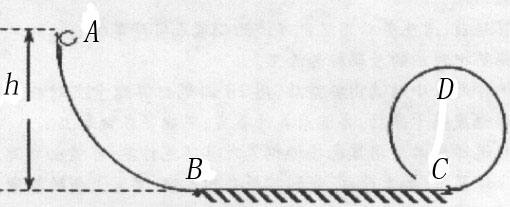
(1)小球滑到B点时和C点时的速度大小;
(2)要使小球能达到圆轨道的最高点D处,则小球在A速度至少为多少?
3、选择题 如图所示,质量相等的两个滑块位于光滑水平桌面上.其中弹簧两端分别与静止的滑块N和挡板P相连接,弹簧与挡板的质量均不计;滑块M以初速度v0向右运动,它与档板P碰撞(不粘连)后开始压缩弹簧,最后,滑块N以速度v0向右运动.在此过程中? (? )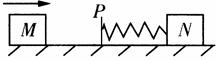
A.M的速度等于0时,弹簧的弹性势能最大
B.M与N具有相同的速度时,两滑块动能之和最小
C.M的速度为v0/2时,弹簧的长度最长
D.M的速度为v0/2时,弹簧的长度最短
4、计算题 (12分)如图所示,在同一竖直平面内两正对着的相同半圆光滑轨道,相隔一定的距离,虚线沿竖直方向,一小球能在其间运动。今在最低点与最高点各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来。当轨道距离变化时,测得两点压力差与距离x的图象如右图所示。(不计空气阻力,g取10m/s2)求: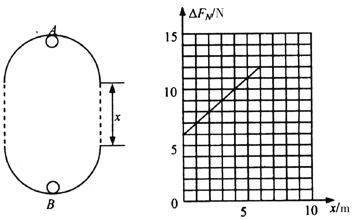
(1)小球的质量;
(2)相同半圆光滑轨道的半径;
(3)若小球在最低点B的速度为20 m/s,为使小球能沿光滑轨道运动,x的最大值。
5、选择题 如图,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面;b球质量为3m, 用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,a可能达到的最大高度为
A.h
B.1.5h
C.2h
D.2.5h