时间:2019-07-03 00:12:02
1、简答题 速度为3m/s的冰壶甲与静止的相同冰壶乙发生对心正碰,碰后甲以1m/s的速度继续向前滑行.求碰后瞬间冰壶乙的速度大小.
参考答案:根据动量守恒定律m1v1+m2v2=m1v1′+m2v2′
代入数据得?v2′=2m/s?
答:碰后瞬间冰壶乙的速度大小为2m/s.
本题解析:
本题难度:一般
2、填空题 如图所示,质量为M、半径为R的光滑圆环静止在光滑的水平面上,有一质量为m的小滑块从与O等高处开始无初速下滑,当到达最低点时,圆环产生的位移大小为______.
参考答案:设滑块滑到最低点所用的时间为t,滑块发生的水平位移大小为R-x,则圆环的位移大小为x,取水平向左方向为正方向.
则根据水平方向平均动量守恒得:m.v1-M.v2=0
即:mR-xt-Mxt=0
解得:x=-mM+mR,负号表示方向向右.
故答案为:mR(M+m);
本题解析:
本题难度:一般
3、简答题 长为L的轻绳,一端用质量为m1的环套在水平光滑的固定横杆AB上,另一端连接一质量为m2的小球,开始时,提取小球并使绳子绷紧转到与横杆平行的位置(如图7)然后同时释放环和小球,当小球自由摆动到最低点时,小球受到绳子的弹力多大? 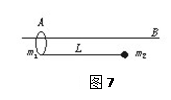
参考答案:3m2g+2m22g/m1
本题解析:对系统分析可知:沿x方向(水平方向)的动量守恒和系统(包括地球)的机械能守恒,则有:
m1v1+m2v2="0?" ①
m1v12/2+m2v22/2=m2gl?②
v1、v2分别为小球摆到最低点时环、球的速度,以向左为正.
联立①②两式,解得:v1=-m2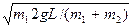 ?/m1
?/m1
v2=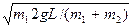 .
.
小球相对于环的速度v21=v2-v1=(1+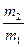
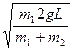 )?③
)?③
又由牛顿第二定律,有
N-m2g=m2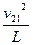 ?④
?④
联立③④式,解得:N=3m2g+2m22g/m1
当m1>>m2时,N=3m2g
本题难度:简单
4、简答题 如图,一辆光滑曲面小车,静止在光滑水平面上,一木块以一定的速度开始沿小车曲面上滑.小车质量为木块质量的4倍,当小车被固定住时,木块沿曲面上滑的最大高度为h.若小车不被固定,则木块沿曲面可上滑的最大高度h"多大?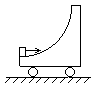
参考答案: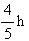
本题解析:
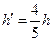
本题难度:简单
5、计算题 一辆小车在光滑的水平面上以v2=1m/s的速度向右运动,小车的质量为M=100kg,如图所示。一质量为m=50kg的人从小车的右端迎面跳上小车,接触小车前瞬间人的水平速度大小为v1=5.6m/s。求人跳上小车后,人和小车共同运动速度的大小和方向。 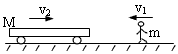
参考答案:解:取向右为正方向 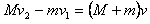
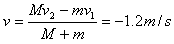
速度大小为1.2m/s,方向向左
本题解析:
本题难度:一般